“理论力学”的版本间的差异
(→刚体动力学) |
|||
| (未显示同一用户的154个中间版本) | |||
| 第1行: | 第1行: | ||
<!-- [[文件:Wiki.gif|right]] --> | <!-- [[文件:Wiki.gif|right]] --> | ||
| + | * [https://www.bilibili.com/video/BV16k4y1B7Rw/ B站网课视频] | ||
| + | * [https://www.bilibili.com/video/BV1MA411v7ej/ B站习题课视频] | ||
参考书籍: | 参考书籍: | ||
#[http://www.amazon.cn/gp/product/B0011C0H0O 朗道,栗弗席兹,《力学(第3版)》(英文影印版),世界图书出版公司] | #[http://www.amazon.cn/gp/product/B0011C0H0O 朗道,栗弗席兹,《力学(第3版)》(英文影印版),世界图书出版公司] | ||
#;朗道十卷本理论物理教程之首。从分析力学讲起,高屋建瓴,推理严密,内容精炼(170页)。可供仔细研读,若感觉难度太高可结合鞠国兴《朗道力学解读》。 | #;朗道十卷本理论物理教程之首。从分析力学讲起,高屋建瓴,推理严密,内容精炼(170页)。可供仔细研读,若感觉难度太高可结合鞠国兴《朗道力学解读》。 | ||
#[http://www.amazon.cn/经典力学/dp/B00475QFVC Goldstein et al.,《经典力学(第3版)》(英文影印版),高等教育出版社] | #[http://www.amazon.cn/经典力学/dp/B00475QFVC Goldstein et al.,《经典力学(第3版)》(英文影印版),高等教育出版社] | ||
| − | #; | + | #;美国普遍采用的理论力学教材,内容丰富,数学推导详尽,有大量习题。内容略多(约630页)。可供选择性阅读,与教材互补。中译本为第2版,内容更加简练,比第3版缺少“混沌”一章。 |
#[http://www.amazon.cn/经典力学的数学方法-V-I-Arnold/dp/B001174V74 Arnold,《经典力学的数学方法》(英文影印版),世界图书出版公司] | #[http://www.amazon.cn/经典力学的数学方法-V-I-Arnold/dp/B001174V74 Arnold,《经典力学的数学方法》(英文影印版),世界图书出版公司] | ||
#;经典名著,内容有深度,数学要求略高。可供查阅。 | #;经典名著,内容有深度,数学要求略高。可供查阅。 | ||
| − | #[ | + | #[https://www.amazon.cn/gp/product/B075GBJ6KP 秦敢、向守平,《力学与理论力学(下册)》,科学出版社] |
| − | #; | + | #;中国科学技术大学的经典教材,以分析力学为主,内容精炼(前四章150页),从易到难,适合于中国学生学习使用。 |
| − | + | ||
== 质点力学 == | == 质点力学 == | ||
| − | === | + | === 质点运动学 === |
---- | ---- | ||
| − | # | + | #运动学变量:坐标 <math> \begin{align}\boldsymbol{r}\end{align} </math>,速度 <math>\boldsymbol{v}=\dot{\boldsymbol{r}}</math>,加速度 <math>\boldsymbol{a}=\dot{\boldsymbol{v}}=\ddot{\boldsymbol{r}}</math>,动量 <math>\boldsymbol{p}=m\boldsymbol{v}</math>,角动量 <math>\boldsymbol{J}=\boldsymbol{r}\times\boldsymbol{p}</math> |
| − | #; | + | #;三种坐标系中运动学变量的具体形式(注意坐标轴方向是否随时间变化) |
##笛卡尔坐标系 <math>\begin{align}\left\{\begin{array}{l} | ##笛卡尔坐标系 <math>\begin{align}\left\{\begin{array}{l} | ||
\boldsymbol{r}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k},\\ | \boldsymbol{r}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k},\\ | ||
| 第26行: | 第27行: | ||
\boldsymbol{a}=(\ddot r-r\dot\theta^2)\boldsymbol{i}+\frac{1}{r}\frac{\rm d}{{\rm d}t}(r^2\dot\theta)\boldsymbol{j}, | \boldsymbol{a}=(\ddot r-r\dot\theta^2)\boldsymbol{i}+\frac{1}{r}\frac{\rm d}{{\rm d}t}(r^2\dot\theta)\boldsymbol{j}, | ||
\end{array}\right. | \end{array}\right. | ||
| − | + | \hspace{7ex} | |
| + | \left\{\begin{array}{l} | ||
\frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\dot\theta \boldsymbol{j},\\ | \frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\dot\theta \boldsymbol{j},\\ | ||
\frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\dot\theta \boldsymbol{i},\end{array} | \frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\dot\theta \boldsymbol{i},\end{array} | ||
| 第32行: | 第34行: | ||
\end{align}</math> | \end{align}</math> | ||
##自然坐标系 <math>\begin{align}\left\{\begin{array}{l} | ##自然坐标系 <math>\begin{align}\left\{\begin{array}{l} | ||
| − | |||
\boldsymbol{v}=\dot s\boldsymbol{i},\\ | \boldsymbol{v}=\dot s\boldsymbol{i},\\ | ||
\boldsymbol{a}=\dot v\boldsymbol{i}+\frac{v^2}{\rho}\boldsymbol{j}=a_{\rm t}\boldsymbol{i}+a_{\rm n}\boldsymbol{j}, | \boldsymbol{a}=\dot v\boldsymbol{i}+\frac{v^2}{\rho}\boldsymbol{j}=a_{\rm t}\boldsymbol{i}+a_{\rm n}\boldsymbol{j}, | ||
\end{array}\right. | \end{array}\right. | ||
| − | + | \hspace{7ex} | |
| + | \left\{\begin{array}{l} | ||
\frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\frac{v}{\rho} \boldsymbol{j},\\ | \frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\frac{v}{\rho} \boldsymbol{j},\\ | ||
\frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\frac{v}{\rho} \boldsymbol{i},\end{array} | \frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\frac{v}{\rho} \boldsymbol{i},\end{array} | ||
\right. | \right. | ||
| + | \end{align} | ||
| + | \hspace{7ex} | ||
| + | \rho=\left|\frac{{\rm d}s}{{\rm d}\theta}\right|=\left|\frac{y^{\prime\prime}}{\left(1+y^\prime\right)^{3/2}}\right|^{-1} | ||
| + | </math> | ||
| + | #;坐标轴随时间变化,则矢量对时间的导数为<math>\begin{align} | ||
| + | \frac{{\rm d}\boldsymbol{G}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{G},~~~~~~~\left(\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}=\dot G_x\hat i+\dot G_y\hat j+\dot G_z\hat k\right) | ||
\end{align}</math> | \end{align}</math> | ||
##;三维欧式空间微分几何(参考苏步青《微分几何学》) | ##;三维欧式空间微分几何(参考苏步青《微分几何学》) | ||
| 第50行: | 第58行: | ||
===质点运动定律=== | ===质点运动定律=== | ||
---- | ---- | ||
| − | + | <ol> | |
| − | # | + | <li>牛顿三定律 |
| − | + | #质点不受其他物体作用 <math>\Longrightarrow {\it p}=</math> 常数 | |
| − | + | #<math>\boldsymbol{F}=m\boldsymbol{a}</math> | |
| − | + | #<math> \boldsymbol{F}_{12}=-\boldsymbol{F}_{21},\boldsymbol{r}_{12}\times\boldsymbol{F}_{12}=0</math> | |
| − | + | </li> | |
| − | + | <li>质点运动微分方程: | |
| − | + | <ol > <li>自由粒子运动微分方程: <math>m\ddot{\boldsymbol{r}}=\boldsymbol{F}(\boldsymbol{r},\dot{\boldsymbol{r}},t)</math>。 | |
| − | + | 分量形式为:<br/> | |
| − | + | {| border="1" cellspacing="0" cellpadding="5" | |
| − | + | | 笛卡尔系 || 平面极坐标系 || 自然坐标系 | |
| + | |- | ||
| + | |<math>\begin{align}\left\{\begin{array}{l} | ||
m\ddot{x}=F_x(x,y,z;\dot x,\dot y,\dot z;t)\\ | m\ddot{x}=F_x(x,y,z;\dot x,\dot y,\dot z;t)\\ | ||
m\ddot{y}=F_y(x,y,z;\dot x,\dot y,\dot z;t)\\ | m\ddot{y}=F_y(x,y,z;\dot x,\dot y,\dot z;t)\\ | ||
m\ddot{z}=F_z(x,y,z;\dot x,\dot y,\dot z;t) | m\ddot{z}=F_z(x,y,z;\dot x,\dot y,\dot z;t) | ||
| − | \end{array}\right.\end{align}</math> | + | \end{array}\right.\end{align}</math> |
| − | + | || | |
| + | <math>\begin{align}\left\{\begin{array}{l} | ||
m(\ddot r-r{\dot\theta}^2)=F_r(r,\theta;\dot r,\dot\theta;t),\\ | m(\ddot r-r{\dot\theta}^2)=F_r(r,\theta;\dot r,\dot\theta;t),\\ | ||
m(r\ddot\theta +2\dot r \dot\theta)=F_\theta(r,\theta;\dot r,\dot\theta;t),\\ | m(r\ddot\theta +2\dot r \dot\theta)=F_\theta(r,\theta;\dot r,\dot\theta;t),\\ | ||
\end{array}\right.\end{align}</math> | \end{array}\right.\end{align}</math> | ||
| − | + | || | |
| + | <math>\begin{align}\left\{\begin{array}{l} | ||
m\dot v=F_{\rm t},\\ | m\dot v=F_{\rm t},\\ | ||
| − | m\frac{v^2}{\rho}=F_{\rm n} | + | m\frac{v^2}{\rho}=F_{\rm n},\\ |
| + | 0=F_{\rm b}. | ||
\end{array}\right.\end{align}</math> | \end{array}\right.\end{align}</math> | ||
| − | + | |} | |
| − | + | </li> | |
| + | <li>非自由粒子运动微分方程:<math>\begin{align}\left\{\begin{array}{l}m\ddot{\boldsymbol{r}}=\boldsymbol{F}(\boldsymbol{r},\dot{\boldsymbol{r}},t)+\boldsymbol{R},\\ | ||
| + | \varphi(\boldsymbol{r})=0~~~(约束方程)\end{array}\right.\end{align}</math><br/> | ||
| + | 分量形式(将<math>\boldsymbol{F}\to \boldsymbol{F}+\boldsymbol{R}</math>) | ||
| + | 自然坐标系:<math>\begin{align}\left\{\begin{array}{l} | ||
m\dot v=F_{\rm t},\\ | m\dot v=F_{\rm t},\\ | ||
m\frac{v^2}{\rho}=F_{\rm n}+R_{\rm n},\\ | m\frac{v^2}{\rho}=F_{\rm n}+R_{\rm n},\\ | ||
| − | 0=F_{\rm b}+R_{\rm b}. | + | 0=F_{\rm b}+R_{\rm b},\\ |
| − | \end{array}\right.\end{align}</math> | + | \varphi(\boldsymbol{r})=0. |
| − | # | + | \end{array}\right.\end{align}</math> |
| − | # | + | </li></ol> |
| − | # | + | </li> |
| + | <li>求解质点运动微分方程的求解方法:(1)数值解法(差分法,适用于线性/非线性、一阶/二阶/高阶、常微分/偏微分等各种方程);(2)解析法. <br/> | ||
| + | 以一维运动为例,运动方程为 <math>m\ddot x=F(x,\dot x,t)</math> | ||
| + | # 如果 <math> F=F(t)</math>,两边直接积分,解为 <math>m (v-v_0)=\int_{t_0}^t F(t){\rm d}t</math> | ||
| + | # 如果 <math> F=F(x)</math>,则将加速度变形为 <math> \ddot x=\frac{1}{2}\frac{{\rm d}\dot x^2}{{\rm d}x} </math>,解为 <math> \frac{m}{2}(v^2-v_0^2)=\int_{x_0}^x F(x){\rm d}x</math> | ||
| + | # 如果 <math> F=F(v)</math>,根据 <math> \ddot x=\dot v</math>,变为一阶方程 <math>m\dot v=F(v) </math>,解为 <math>\int_{v_0}^v\frac{{\rm d}v}{F(v)}=t-t_0</math> | ||
| + | # 如果 <math> F=g(x)h(v)</math>,根据上边加速度的表示式 <math> \ddot x=v\frac{{\rm d}v}{{\rm d}x}</math>,得到 <math>mv\frac{{\rm d}v}{{\rm d}x}=g(x)h(v)</math>,为可分离变量的一阶微分方程,解为 <math>\int_{v_0}^{v} \frac{v{\rm d}v}{h(v)}=\int_{x_0}^x g(x){\rm d}x</math> | ||
| + | # 如果 <math> F=h(v)f(t) </math>,根据 <math> \ddot x=\dot v</math>,解为 <math>\int_{v_0}^v\frac{{\rm d}v}{h(v)}=\int_{t_0}^t f(t){\rm d}t</math> | ||
| + | </li></ol> | ||
===质点运动定理=== | ===质点运动定理=== | ||
---- | ---- | ||
| − | + | <ol> | |
| − | # | + | <li>保守力:如果 <math>\boldsymbol{F}</math> 做功与路径无关,只依赖于出发点和终点坐标,则 <math>\boldsymbol{F}</math> 叫保守力。<br/> |
| − | # | + | 保守力的四个等效条件: |
| − | + | # 从 A 到 B 点的曲线积分 <math>\int_A^B \boldsymbol{F}\cdot{\rm d}\boldsymbol{r}</math> 仅依赖于端点 A 和 B ,与路径无关. | |
| − | + | # 沿封闭路径的曲线积分<math>\oint_L\boldsymbol{F}\cdot{\rm d}\boldsymbol{r}=0</math> | |
| − | + | # 满足 <math>\nabla\times \boldsymbol{F}=0</math> | |
| − | + | # 存在标量函数 <math>V(\boldsymbol{r})</math> 满足 <math>\boldsymbol{F}=-\nabla V(r)</math> | |
| − | + | 物理上,标量函数 <math>V(\boldsymbol{r})</math> 即为保守力 <math>\boldsymbol{F}</math> 对应的势能。 | |
| − | + | <br/>保守力:conservative force,原始意义是保持系统能量守恒(conserved)的作用力。(见朗道第 <math>\S6</math> 节)</li> | |
| − | + | ||
| + | <li>质点运动定理和守恒定律 | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="5" | ||
| + | |运动定理 || 积分和微分形式 || 运动守恒律 || 内容 | ||
| + | |- | ||
| + | |动量定理 || <math>\dot{\boldsymbol{p}}=\boldsymbol{F}</math> , <math>{\rm d}\boldsymbol{p}={\rm d}\boldsymbol{F}{\rm d}t</math> ||动量守恒定律 || <math>\boldsymbol{F}=0\Longrightarrow\boldsymbol{p}=</math>常数 | ||
| + | |- | ||
| + | |角动量定理 || <math>\dot{\boldsymbol{J}}=\boldsymbol{M}</math> , <math>{\rm d}\boldsymbol{J}=\boldsymbol{M}{\rm d}t</math> || 角动量守恒定律 || <math>\boldsymbol{M}=0\Longrightarrow \boldsymbol{J}=</math>常数 | ||
| + | |- | ||
| + | |动能定理 || <math>{\rm d}T=\boldsymbol{F}\cdot{\rm d}\boldsymbol{r}</math> (动能 <math>T\equiv \frac{1}{2}mv^2</math>)|| 机械能守恒定律 || <math> \boldsymbol{F} </math> 为保守力 <math>\Longrightarrow E=</math>常数 (总能量 <math>E=T+V</math>) | ||
| + | |} | ||
| + | </li> | ||
| + | </ol> | ||
===有心力=== | ===有心力=== | ||
| 第100行: | 第138行: | ||
---- | ---- | ||
| − | #质点在有心力场中运动 <math>\Longrightarrow</math> | + | #质点在有心力场中运动 <math>\Longrightarrow</math> <span style="color: blue">'''角动量守恒'''</span>(<math>\boldsymbol{J}=\boldsymbol{C}_1</math>)<math>\Longrightarrow</math> 平面运动 |
| − | #有心力必定为保守力,<math>\boldsymbol{F}=-\nabla U(r)</math>,其中 <math>U(r)</math> 为势能 | + | #有心力必定为保守力,<math>\boldsymbol{F}=-\nabla U(r)</math>,其中 <math>U(r)</math> 为势能 <math>\Longrightarrow </math> <span style="color: blue">'''机械能守恒'''</span> (<math>E=T+U(r)=C_2</math>) |
#质点在有心力场中的运动等价于一维运动:<math>m\ddot r=-\nabla V(r)</math><math>~~~~~\left(V(r)=U(r)+\frac{\boldsymbol{J}^2}{2mr^2}\right)</math> | #质点在有心力场中的运动等价于一维运动:<math>m\ddot r=-\nabla V(r)</math><math>~~~~~\left(V(r)=U(r)+\frac{\boldsymbol{J}^2}{2mr^2}\right)</math> | ||
| − | #轨道有限的条件:有效势能<math>V(r)</math>存在势阱,能量<math>E</math>小于势阱两边势垒的高度,从而质点能够束缚在势阱中运动。 | + | #轨道有限的条件:有效势能<math>V(r)</math>存在势阱,能量<math>E</math>小于势阱两边势垒的高度,从而质点能够束缚在势阱中运动。 <br />假设势能取幂函数形式,<math>U(r)=cr^\alpha</math>,根据上述条件有<math>V^\prime(r)=0,V^{\prime\prime}(r)>0</math>,从而得到轨道有限的必要条件为<math>\begin{align}\left\{\begin{array}{ll} |
| − | + | ||
c>0,&\alpha>0,\\ | c>0,&\alpha>0,\\ | ||
c<0,&-2<\alpha<0 | c<0,&-2<\alpha<0 | ||
\end{array}\right.\end{align}</math> | \end{array}\right.\end{align}</math> | ||
| − | # | + | #轨道方程:<math>\theta=\int \frac{J/r^2{\rm d}r}{\sqrt{2m(E-V(r))}} </math>;质点在有心力场中运动的轨道封闭的条件:<math>\Delta\theta=2\int_{r_{\rm min}}^{r_{\rm max}}\frac{J/r^2{\rm d}r}{\sqrt{2m(E-V(r))}}=\pi \times</math>有理数 |
| − | # | + | #圆形轨道的稳定性:从等效一维运动的角度讨论,稳定性意味着粒子束缚在一个势阱中运动。因此稳定性条件与前边的有限性条件相同。 |
| − | + | #万有引力(平方反比引力)作用下运动方程的解:<math>r=\frac{p}{1+e\cos\theta}.\hspace{3ex}\left(p=\frac{J^2}{mk^2},e=\sqrt{1+\frac{2EJ^2}{mk^4}}\right)</math> | |
| − | + | #平方反比斥力:<math>\alpha</math> 粒子的散射,运动方程的解为 <math> r=\frac{p}{e\cos\theta-1}.\hspace{3ex}\left(p=\frac{J^2}{mk^2},e=\sqrt{1+\frac{2EJ^2}{mk^4}}\right)</math>. | |
| − | #万有引力(平方反比引力)作用下运动方程的解:<math>r=\frac{p}{1+e\cos\theta}</math> | + | |
| − | #平方反比斥力:<math>\alpha</math> | + | |
| − | + | ||
| − | + | ||
#扩展(SRT和毕业论文候选) | #扩展(SRT和毕业论文候选) | ||
| − | ## | + | ##双恒星系统中行星的轨道?居住在行星上的人的历法会如何发展? |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | === 常用数学公式 === | ||
---- | ---- | ||
| + | <ol > | ||
| + | <li><math> \begin{align} | ||
| + | \int\frac{{\rm d}x}{1+x^2}&=\arctan x+C,& \int\frac{{\rm d}x}{\sqrt{1+x^2}}&={\rm arcsinh}\, x+C,\\ | ||
| + | \int\frac{{\rm d}x}{1-x^2}&={\rm arctanh}\,x+C,& \int\frac{{\rm d}x}{\sqrt{1-x^2}}&=\arcsin x+C. | ||
| + | \end{align} | ||
| + | </math></li> | ||
| − | + | <li>二阶常系数齐次线性微分方程 <math> \ddot x+p\dot x+q x=0</math>,解的形式取决于特征方程 <math> r^2+pr+q=0</math> 解的情况。<br/> | |
| − | + | <math>\begin{align}x(t)=\left\{\begin{array}{ll} | |
| − | + | C_1 e^{r_1 t}+C_2 e^{r_2 t},& (2~个不同实根~ r_1\neq r_2)\\ | |
| + | \left(C_1+C_2t\right)e^{rt},& (2重实根~ r_1=r_2\equiv r)\\ | ||
| + | e^{\alpha t}\left(C_1\cos\beta t+C_2\sin\beta t\right),&(2~个共轭复根~ r_{1,2}=\alpha\pm i\beta) | ||
| + | \end{array}\right.\end{align}</math></li> | ||
| + | |||
| + | <li>二阶常系数非齐次线性微分方程 <math> \ddot x+p\dot x+q x=f(t)</math>,通解为 <math>x=x^*+X</math>,其中 <math>X</math> 是对应的齐次方程即当 <math>f(t)=0</math> 的时候方程的通解,而 <math> x^* </math> 是非齐次方程的特解。当 <math>f(t)=e^{ct}P_n(t) </math> 时(<math>P_n(t) </math> 为 <math>t</math> 的<math>n</math> 次多项式,<math>c</math> 为复数),特解 <math>x^* </math> 有简单的形式。<br/> | ||
| + | 取 <math>f(t)=e^{\lambda t}\left(P_n(t)\cos\omega t+P_l(t)\sin\omega t\right)</math>,则 | ||
| + | <math>\begin{align}x^*=\left\{\begin{array}{l@{~~~~~}l} | ||
| + | e^{\lambda t}\left(Q_m(t)\cos\omega t+R_m(t)\sin\omega t\right),&\left(\lambda+i\omega\text{不是特征方程}r^2+pr+q=0\text{的根}\right)\\ | ||
| + | te^{\lambda t}\left(Q_m(t)\cos\omega t+R_m(t)\sin\omega t\right),&\left(\lambda+i\omega\text{是特征方程}r^2+pr+q=0\text{的根}\right) | ||
| + | \end{array}\right.\end{align}</math> | ||
| + | 上式中 <math>Q_m(t)=a_0+a_1 t+\ldots +a_m t^m,~~~R_m(t)=b_0+b_1 t+\ldots+b_m t^m</math>,其中 <math>m={\rm max}(l,n)</math>。将 <math> Q_m(t),~R_m(t)</math> 的形式代回原非齐次方程,让对应项的系数相等从而解出 <math>a_1,a_2,\ldots,a_m,b_1,b_2,\ldots,b_m</math>。这样方程的通解 <math>x=x^*+X</math> 就完全解出。 | ||
| + | </li> | ||
| + | |||
| + | <li>一阶微分方程 <br/> | ||
| + | <math>\begin{align}\begin{array}{|l|@{~~~}l|@{~~~}l|}\hline | ||
| + | \text{方程类型} & \text{方程形式} & \text{方程通解}\\\hline | ||
| + | \text{可分离变量} & y^\prime=g(x)h(y) & \int\frac{{\rm d}y}{h(y)}=\int g(x){\rm d}x+C\\\hline | ||
| + | \text{齐次微分方程} & y^\prime=\varphi\left(\frac{y}{x}\right) & \int\frac{{\rm d}\tilde y}{\varphi(\tilde y)-\tilde y}=\ln x+C,~~~\left(\tilde y\equiv\frac{y}{x}\right)\\\hline | ||
| + | \text{线性微分方程} & y^\prime+P(x)+Q(y)=0 & y=e^{-\int P(x){\rm d}x}\left[-\int Q(x)e^{\int P(x){\rm d}x}{\rm d}x+C\right]\\\hline | ||
| + | \text{伯努利方程} & y^\prime+P(x)y+Q(y) y^n=0 & \frac{1}{1-n}\tilde y^\prime+P(x)\tilde y+Q(x)=0,~~~(\tilde y=y^{1-n})\\\hline | ||
| + | \end{array}\end{align}</math> | ||
| + | </li> | ||
| + | |||
| + | </ol> | ||
== 质点组力学 == | == 质点组力学 == | ||
| − | === | + | ===质点组力学框架=== |
---- | ---- | ||
| − | # | + | #运动学: |
| − | + | #*质点组总动量:<math>\boldsymbol{p}=m\boldsymbol{v}_c+\boldsymbol{0}</math> | |
| − | # | + | #*质点组总角动量:<math>\begin{align} \boldsymbol{J}=\boldsymbol{r}\times m\boldsymbol{v}_c+\boldsymbol{J}^\prime\end{align}</math> |
| − | # | + | #*质点组总动能(柯尼希定理):<math>\begin{align} T=\frac{1}{2}m\boldsymbol{v}_c^2+T^\prime\end{align}</math>,即<math>\begin{align}\frac{1}{2}\sum_{i=1}^n m_i \dot{\boldsymbol{r}}_i^{2}=\frac{1}{2}m\dot{\boldsymbol{r}}_C^2+\frac{1}{2}\sum_{i=1}^n m_i \dot{\boldsymbol{r}}_i^{\prime 2}\end{align}</math>,其中 <math>\begin{align} m=\sum_{i=1}^n m_i \end{align}</math> |
| + | #动力学 | ||
| + | #*质点组动量定理:<math>\begin{align} {\rm d}\boldsymbol{p}=\left(\sum_{i=1}^n \boldsymbol{F}_i^{(\rm e)}\right){\rm d}t \end{align}</math> | ||
| + | #*质点组角动量定理:<math>\begin{align} {\rm d}\boldsymbol{J}=\left(\sum_{i=1}^n \boldsymbol{M}_i^{(\rm e)}\right){\rm d}t \end{align}</math> | ||
| + | #*质点组动能定理:<math>\begin{align} {\rm d}T=\sum_{i=1}^n \boldsymbol{F}_i^{(\rm e)}\cdot {\rm d}\boldsymbol{r}_i+\sum_{i=1}^n \boldsymbol{F}_i^{(\rm i)}\cdot {\rm d}\boldsymbol{r}_i \end{align}</math> | ||
=== 两体问题 === | === 两体问题 === | ||
---- | ---- | ||
| − | + | 两质点组成的系统,如果合外力为 0 即 <math>0=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_2^{(\rm e)}</math>,对每个质点分别列运动方程:<math>\begin{align}\left\{\begin{array}{l} | |
| − | m_1\ddot{\boldsymbol{r}}_1=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F} | + | m_1\ddot{\boldsymbol{r}}_1=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)},\\ |
| − | m_2\ddot{\boldsymbol{r}}_2=\boldsymbol{F}_2^{(\rm e)}+\boldsymbol{F} | + | m_2\ddot{\boldsymbol{r}}_2=\boldsymbol{F}_2^{(\rm e)}+\boldsymbol{F}_{12}^{(\rm i)}, |
\end{array}\right.\end{align}</math> | \end{array}\right.\end{align}</math> | ||
| − | + | ,其中 <math>\boldsymbol{F}_{21}^{(\rm i)}=-\boldsymbol{F}_{12}^{(\rm i)}</math>。 | |
| − | + | #两式之和为质心运动微分方程:<math>\begin{align}m\ddot{\boldsymbol{r}}_c=0,\hspace{2ex}\left(m=m_1+m_2\right)\end{align}</math> | |
#; | #; | ||
| − | #两式分别乘以 <math>m_2</math> 和 <math>m_1</math>,相减得到:<math>m_1m_2\left(\ddot{\boldsymbol{r}}_1-\ddot{\boldsymbol{r}}_2\right)=m_2\ | + | #两式分别乘以 <math>m_2</math> 和 <math>m_1</math>,相减得到:<math>m_1m_2\left(\ddot{\boldsymbol{r}}_1-\ddot{\boldsymbol{r}}_2\right)=(m_1+m_2)\left(\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)}\right)</math>,即 <math>\mu\ddot{\boldsymbol{r}}=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)}</math>,其中 <math>\boldsymbol{r}\equiv \boldsymbol{r}_1-\boldsymbol{r}_2</math>为两质点的相对位矢, <math>\mu\equiv \frac{m_1m_2}{m_1+m_2}</math> 叫做折合质量。<br />如果两质点不受外力,且两质点相互作用力仅依赖于距离(是保守力),那么 <math>\boldsymbol{F}_{21}^{(\rm i)}=-\nabla U(\boldsymbol{r})</math>,<math>\big(U(\boldsymbol{r})</math> 为两质点相互作用势能<math>\big)</math>,上式可化为有心力场中的单质点运动问题 <math>\begin{align} \mu \ddot{\boldsymbol{r}}=-\nabla U(\boldsymbol{r})\end{align}</math>。 |
| − | + | ||
| − | + | 简言之,不受外力的两质点的运动,可以等价为<span style="color: blue">'''质心的匀速直线运动'''</span>与<span style="color: blue">'''具有折合质量的质点的相对运动'''</span>的合成,运动方程分别为 | |
| + | <math>\begin{align}\left\{\begin{array}{l} | ||
| + | m\ddot{\boldsymbol{r}}_c=0,\\ | ||
| + | \mu\ddot{\boldsymbol{r}}=-\nabla U(\boldsymbol{r}). | ||
| + | \end{array}\right.\end{align}</math> | ||
| + | |||
| + | === 变质量物体运动方程 === | ||
| + | ---- | ||
| + | <math>\begin{align} \frac{{\rm d}}{{\rm d}t}\left(m\boldsymbol{v}\right)-\dot m \boldsymbol{v}=\boldsymbol{F}.\end{align}</math> | ||
=== 位力定理 === | === 位力定理 === | ||
---- | ---- | ||
| − | + | 对于满足'''坐标和动量均取有限值'''的运动(包括周期性运动),质点组动能的时间平均值等于位力积时间平均值的负值。即 | |
<math>\overline{T}=-\frac{1}{2}\overline{\sum_{i=1}^n\boldsymbol{F}_i\cdot\boldsymbol{r}_i}</math> | <math>\overline{T}=-\frac{1}{2}\overline{\sum_{i=1}^n\boldsymbol{F}_i\cdot\boldsymbol{r}_i}</math> | ||
| − | + | 如果势能是坐标的 <math>n</math>次函数,即 <math>V(\boldsymbol{r})=cr^n</math>,则 <math>\boldsymbol{r}\cdot\nabla V(\boldsymbol{r})=nV(\boldsymbol{r})</math>。因此我们得到 | |
| + | <math>\overline{T}=\frac{n}{2}\overline{V}</math> | ||
| − | = | + | 在统计力学中,位力定理可以导出理想气体状态方程 <math>PV=nRT</math>,也是可以系统地导出非理想气体状态方程;在量子力学中位力定理也有重要应用。更详细的讨论见 [https://en.wikipedia.org/wiki/Virial_theorem 位力定理] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== 刚体力学 == | == 刚体力学 == | ||
| 第172行: | 第238行: | ||
---- | ---- | ||
| + | <ol> | ||
| − | + | <li>刚体有6个自由度,可以取为刚体上的一点O的位矢 <math>\boldsymbol{r}_O</math> 和转动的角度即三个欧拉角 <math>\theta,~~\varphi,~~~\psi</math>。刚体一般运动为参考点O的平动与绕参考点转动的合成。</li> | |
| − | + | <li>一般取固定在刚体上的三个相互垂直的轴为坐标轴,建立随刚体运动的坐标系<math>o-xyz</math>。(注意:参考系一般选取地面静止系,与坐标系要区分开) | |
| + | <br/>刚体的位置可用欧拉角描述,他们分别为进动角 <math>\varphi</math>、自转角 <math>\psi</math>、章动角 <math>\theta</math> : | ||
| + | <br/> <br/>[[文件:欧拉角.png|300px]]<br/> </li> | ||
| + | |||
| + | <li><span style="color: blue">'''欧拉运动学方程'''</span>:<br/> | ||
| + | |||
| + | <math>\begin{align}\left\{\begin{array}{l} | ||
\omega_x=\dot\varphi\sin\theta\sin\psi+\dot\theta\cos\psi,\\ | \omega_x=\dot\varphi\sin\theta\sin\psi+\dot\theta\cos\psi,\\ | ||
\omega_y=\dot\varphi\sin\theta\cos\psi-\dot\theta\sin\psi,\\ | \omega_y=\dot\varphi\sin\theta\cos\psi-\dot\theta\sin\psi,\\ | ||
\omega_z=\dot\varphi\cos\theta+\dot\psi, | \omega_z=\dot\varphi\cos\theta+\dot\psi, | ||
| − | \end{array}\right.\end{align}</math> | + | \end{array}\right.\end{align}</math> |
| − | + | <br>上式来源于 <math>\boldsymbol{\omega}=\dot\varphi\boldsymbol{e}_\zeta+\dot\theta\boldsymbol{e}_{ON}+\dot\psi \boldsymbol{e}_z</math>,其中 <math>\zeta</math> 轴和 <math>ON</math> 轴的方位角和极角分别为 <math>\left(\theta,\frac{\pi}{2}-\psi\right)</math> 和 <math>\left(\frac{\pi}{2},-\psi\right)</math> 。刚体转动方向的三个单位矢量在刚体随动系中的表达式为<math>\begin{align}\left\{\begin{array}{l} | |
| − | \boldsymbol{e}_\zeta=\sin\theta\ | + | \boldsymbol{e}_\zeta=\sin\theta\sin\psi\boldsymbol{i}+\sin\theta\cos\psi\boldsymbol{j}+\cos\theta\boldsymbol{k},\\ |
| − | \boldsymbol{e} | + | \boldsymbol{e}_{ON}=\cos\psi\boldsymbol{i}-\sin\psi\boldsymbol{j},\\ |
\boldsymbol{e}_z=\boldsymbol{k}, | \boldsymbol{e}_z=\boldsymbol{k}, | ||
| − | \end{array}\right.\end{align}</math> | + | \end{array}\right.\end{align}</math> <br/>刚体角速度为矢量,按照普通矢量相加 <math>\boldsymbol{\omega}=\boldsymbol{\omega}_1+\boldsymbol{\omega}_2</math></li> |
| − | = | + | <li> 刚体转动惯量张量为 <br/> |
| + | <math>\begin{align}\hat I=\left(\begin{array}{ccc} | ||
| + | \hat I_{xx} & \hat I_{xy} & \hat I_{xz}\\ | ||
| + | \hat I_{xy} & \hat I_{yy} & \hat I_{yz}\\ | ||
| + | \hat I_{xz} & \hat I_{yz} & \hat I_{zz} | ||
| + | \end{array}\right)\end{align}</math> | ||
| − | ---- | + | 其中惯量张量矩阵元的一般定义式为 |
| + | <math>\begin{align}\hat I_{ij}=\int \left(\boldsymbol{r}^2\delta_{ij}-r_ir_j\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r}\end{align}</math>,即<br/> | ||
| + | <math>\begin{align}\hat I_{xx}=\int\left(y^2+z^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ | ||
| + | \hat I_{yy}=\int\left(x^2+z^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ | ||
| + | \hat I_{zz}=\int\left(x^2+y^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\end{align}\hspace{5ex}</math> | ||
| + | <math>\begin{align}\hat I_{xy}=-\int xy\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ | ||
| + | \hat I_{yz}=-\int yz\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ | ||
| + | \hat I_{xz}=-\int xz\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r}.\end{align}</math><br> | ||
| + | 注意这里的定义与周衍柏教材中的定义的对应:对角元相等,即<math>\hat I_{xx}=I_{xx},\hat I_{yy}=I_{yy},\hat I_{zz}=I_{zz}</math>;非对角元相差一个负号,即<math>\hat I_{xy}=-I_{xy},\hat I_{yz}=-I_{yz},\hat I_{xz}=-I_{xz}</math> | ||
| + | </li> | ||
| − | + | <li>作定点运动的刚体,角动量为 <math>\boldsymbol{J}=\hat{\boldsymbol{I}}\cdot\boldsymbol{\omega}</math>,动能为<math>T=\frac{1}{2}\boldsymbol{\omega}\cdot\boldsymbol{\hat I}\cdot\boldsymbol{\omega}</math>。<br> | |
| − | + | 在刚体的本体坐标系中,角动量和动能可以写为 <math>\begin{align} | |
| − | + | ||
| − | \ | + | |
| − | + | ||
\left(\begin{array}{l}J_x\\J_y\\J_z\end{array}\right) | \left(\begin{array}{l}J_x\\J_y\\J_z\end{array}\right) | ||
| − | =\left(\begin{array}{rrr}I_{xx}& | + | =\left(\begin{array}{rrr}\hat I_{xx}&\hat I_{xy}&\hat I_{xz}\\\hat I_{yx}&\hat I_{yy}&\hat I_{yz}\\\hat I_{zx}&\hat I_{zy}&\hat I_{zz}\end{array}\right) |
| − | \left(\begin{array}{l}\omega_x\\\omega_y\\\omega_z\end{array}\right)\end{align}</math> | + | \left(\begin{array}{l}\omega_x\\\omega_y\\\omega_z\end{array}\right)\end{align}</math> <br> |
| − | + | <math>T=\frac{1}{2}(\hat I_{xx}\omega_x^2+\hat I_{yy}\omega_y^2+\hat I_{zz}\omega_z^2+2\hat I_{xy}\omega_x\omega_y+2\hat I_{yz}\omega_y\omega_z+2\hat I_{xz}\omega_x\omega_z)=\frac{1}{2}I_n\omega^2</math>,其中 <math>\vec\omega=\omega\hat e_n</math>,<math>I_n\equiv \boldsymbol{n}\cdot\hat{\boldsymbol{I}}\cdot\boldsymbol{n}</math> 为刚体对过定点且沿 <math>\boldsymbol{n}</math> 方向的转轴的转动惯量。<br/> | |
| − | + | 空间转动变换,可以将转动惯量张量 <math>\hat{\boldsymbol{I}}</math> 对角化,此时的坐标轴为惯量主轴。<br/>惯量主轴的求解:惯量椭球 <math>\boldsymbol{r}\cdot\hat{\boldsymbol{A}}\cdot\boldsymbol{r}=1</math> 的三个对称轴。</li> | |
| − | + | ||
| − | = | + | <li>刚体上任意一点的速度:<math>\boldsymbol{ v}_A=\boldsymbol{ v}_O+\boldsymbol{\omega}\times\boldsymbol{ r}_{OA}</math></li> |
| − | + | <li>刚体的动能有两部分组成:质心动能和转动动能,即<math>T=\frac{1}{2}m\boldsymbol{v}_c^2+\frac{1}{2}I_n\omega^2</math></li> | |
| − | + | </ol> | |
| − | + | ||
| − | + | ||
| − | === | + | === 刚体动力学 === |
---- | ---- | ||
| + | 刚体动力学方程包括刚体动量定理、刚体角动量定理(即欧拉动力学方程)和刚体动能定理。 | ||
| − | + | <ol> | |
| − | + | <li> 刚体动量定理:<math>m\ddot{\boldsymbol{r}}_c=\boldsymbol{F}</math>,刚体质心运动由刚体受到的合外力决定。</li> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | <li> 刚体角动量定理:<math>\dot{\boldsymbol{J}}=\boldsymbol{M}</math>,其中角动量 <math>\boldsymbol{J}=\hat{\boldsymbol{A}}\cdot\boldsymbol{\omega}</math>。为简化计算,欧拉采用了两重简化方式 |
| + | * 采用固定在刚体上的坐标系,则转动惯量张量 <math>{\rm d}\hat{\boldsymbol{A}}/{\rm d}t=0</math>,角速度 <math>\boldsymbol{\omega}=\omega_x\boldsymbol{i}+\omega_y\boldsymbol{j}+\omega_z\boldsymbol{k}</math>,其中坐标轴的单位矢量随时间变化,满足 | ||
| + | <math>\begin{align}\frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=\boldsymbol{\omega}\times\boldsymbol{i},~~~ | ||
| + | \frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=\boldsymbol{\omega}\times\boldsymbol{j},~~~ | ||
| + | \frac{{\rm d}\boldsymbol{k}}{{\rm d}t}=\boldsymbol{\omega}\times\boldsymbol{k}\end{align},</math> | ||
| + | 用<math>\boldsymbol{i,j,k}</math>展开的任意矢量<math>\boldsymbol{G}=G_x\boldsymbol{i}+G_y\boldsymbol{j}+G_z\boldsymbol{k}</math>,对时间的导数为<math>\begin{align}\frac{{\rm d}\boldsymbol{G}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{G}\end{align}</math>。因此刚体角动量定理变为:<br /> | ||
| + | <br/><math>\begin{align}\frac{{\rm d}^*\boldsymbol{J}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{J}=\boldsymbol{M}.\end{align}</math> | ||
| + | * 取<math>o-xyz</math>的坐标轴为刚体的惯量主轴,则惯量张量为对角矩阵即<math>\begin{align}\hat{\boldsymbol{A}}=\left(\begin{array}{ccc} | ||
| + | I_1 & 0 & 0\\ | ||
| + | 0 & I_2 & 0\\ | ||
| + | 0 & 0 & I_3 | ||
| + | \end{array}\right)\end{align}</math> | ||
| + | 因此角动量形式为 <math>\begin{align}\boldsymbol{J}=\hat{\boldsymbol{A}}\cdot\boldsymbol{\omega}=I_1\omega_x\boldsymbol{i}+I_2\omega_y\boldsymbol{j}+I_3\omega_z\boldsymbol{k}\end{align}</math>。代入刚体角动量定理,其分量形式即为<span style="color: blue">'''欧拉动力学方程 '''</span> | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{l} | ||
| + | I_1\dot\omega_x+(I_3-I_2)\omega_y\omega_z=M_x,\\ | ||
| + | I_2\dot\omega_y+(I_1-I_3)\omega_z\omega_x=M_y,\\ | ||
| + | I_3\dot\omega_z+(I_2-I_1)\omega_x\omega_y=M_z. | ||
| + | \end{array}\right.\end{align}</math><br/></li> | ||
| − | + | <li> 刚体动能定理:<math>\begin{align}{\rm d}T=\sum_{i=1}^n\boldsymbol{F}^{(\rm e)}_i\cdot{\rm d}\boldsymbol{r}_i\end{align}</math>,其中刚体动能为<math>T=\frac{1}{2}mv_c^2+\frac{1}{2}I_n\omega^2</math></li> | |
| + | </ol> | ||
| − | # | + | === 刚体运动分类 === |
| − | # | + | |
| − | # | + | ---- |
| + | <ol> | ||
| + | <li> 刚体平动:欧拉角为常数,角速度<math>\boldsymbol{\omega}=0</math>。自由度数 <math> s=3</math>,取为刚体质心位矢。 </li> | ||
| + | <li> 刚体定轴转动:刚体上一点固定,且角速度仅沿一个方向。自由度数 <math>s=1</math>,取为自转角。<br> | ||
| + | 把角速度方向取为z方向,则<math>\omega_x=\omega_y=0</math>,角动量简化为 <math>\boldsymbol{J}=I_{xz}\omega_z\boldsymbol{i}+I_{yz}\omega_z\boldsymbol{j}+I_{zz}\omega_z\boldsymbol{k}</math>,刚体的角动量定理变为<br /> | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{r} | ||
| + | I_{xz}\dot\omega_z-I_{yz}\omega_z^2=M_x,\\ | ||
| + | I_{yz}\dot\omega_z+I_{xz}\omega_z^2=M_y,\\ | ||
| + | I_{zz}\dot\omega_z=M_z, | ||
| + | \end{array}\right.\end{align}</math> <br/> 最后一式是动力学方程,前两式可以用来求解对刚体转轴的约束力。 | ||
| + | </li> | ||
| + | <li> 刚体平面平行运动:刚体上一点做平面运动,且刚体角速度垂直于这个平面。自由度数 <math> s=3 </math>,取为刚体上一点在平面内的位矢和刚体的转动角度。<br/> | ||
| + | 刚体的角动量定理同上,动量定理只涉及x和y方向,即<math>\begin{align}\left\{\begin{array}{l} | ||
| + | m\ddot{\boldsymbol{x}}_c=\boldsymbol{F}_x,\\ | ||
| + | m\ddot{\boldsymbol{y}}_c=\boldsymbol{F}_y, | ||
| + | \end{array}\right.\end{align}</math><br/> | ||
| + | 平面平行运动的刚体必有转动瞬心<math>O</math>。转动瞬心可以简化刚体的运动描述 | ||
| + | # 刚体的总动能可以写为 <math>T=\frac{1}{2}I_O\omega^2</math> ,<math>I_O</math> 是绕瞬心的转动惯量 | ||
| + | # 刚体上一点的速度可以写为 <math>\boldsymbol{v}=\boldsymbol{\omega}\times\boldsymbol{r}^\prime</math>,<math>\boldsymbol{r}^\prime</math> 是该点相对于转动瞬心的相对位矢。<br/> | ||
| + | 转动瞬心的求法: | ||
| + | # 已知刚体上两点速度,如果速度方向不同,则瞬心为两速度垂线的交点; | ||
| + | # 已知刚体上一点速度和刚体角动量,则瞬心位于过该点且垂直于速度的直线上,且与该点的距离为<math> \frac{v}{\omega}</math>; | ||
| + | # 已知两点的速度,速度方向相同,且过一点速度的垂线穿过第二点,则可以建立相似三角形确定速度; | ||
| + | # 如果两点速度平行且速度的垂涎穿过两点,则刚体的转动瞬心在无穷远处。 | ||
| + | <br/> | ||
| + | [[文件:瞬心-1.png|150px]][[文件:瞬心-2.png|135px]]<math>\hspace{3ex}</math>[[文件:瞬心-3.png|165px]][[文件:瞬心-4.png|165px]] | ||
| + | <br/> | ||
| + | 转动瞬心划过的轨迹,在地面静止系中叫做空间极迹;在刚体静止系中叫做本体极迹。 | ||
| + | </li> | ||
| + | <li> 刚体定点转动:刚体上有一固定点O,角速度无限制。自由度数 <math>s=3</math>,取为刚体的三个欧拉角。<br/> | ||
| + | 刚体定点运动的动力学方程完整的<span style="color: blue">'''欧拉动力学方程'''</span>。<br/> | ||
| + | 重刚体:主动力仅有重力的刚体。有解析解的重刚体有三种: | ||
| + | <ol> | ||
| + | <li> 欧拉-潘索情况:外力通过固定点O,<math>\boldsymbol{M}=0</math>,刚体在惯性下运动。欧拉动力学方程简化为 | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{l} | ||
| + | I_1\dot\omega_x-(I_2-I_3)\omega_y\omega_z=0,\\ | ||
| + | I_2\dot\omega_y-(I_3-I_1)\omega_z\omega_x=0,\\ | ||
| + | I_3\dot\omega_z-(I_1-I_2)\omega_x\omega_y=0. | ||
| + | \end{array}\right.\end{align}</math><br/> | ||
| + | 根据上述方程,可以求出<math>\omega_x,\omega_y,\omega_z</math>;再利用欧拉动力学方程,求出欧拉角随时间变化的方程<math>\theta(t),\varphi(t),\psi(t)</math>。这样运动方程就完全解出。<br/> | ||
| + | 当<math>I_1=I_2</math>的特殊情况下(比如地球),运动方程可以得到简化。<br/> | ||
| + | 潘索引入了几何方法,可以比较简便的说明一般情况下(<math>I_1\neq I_2\neq I_3</math>)刚体的运动图像。</li> | ||
| + | <li> 拉格朗日-泊松情况(对称陀螺):重力作用点不过固定点O,但有<math>I_1=I_2</math>。欧拉动力学方程化简为 | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{l} | ||
| + | I_1\dot\omega_x-(I_1-I_3)\omega_y\omega_z=mgl\sin\theta\cos\psi,\\ | ||
| + | I_1\dot\omega_y+(I_3-I_1)\omega_z\omega_x=mgl\sin\theta\sin\psi,\\ | ||
| + | I_3\dot\omega_z=0. | ||
| + | \end{array}\right.\end{align}</math><br/> | ||
| + | 根据欧拉运动学方程,易得对称陀螺的拉格朗日函数 <math>\begin{align}L=\frac{1}{2}I_1\left(\dot\theta^2+\sin^2\theta\dot\varphi^2\right)+\frac{1}{2}I_3\left(\cos\theta\dot\varphi+\dot\psi\right)^2-mgl\cos\theta\end{align}</math>。因为拉格朗日函数对<math>\varphi</math>和<math>\psi</math>没有依赖,因此对应的广义动量为一次积分(守恒量);同时,因为动量是广义速度的二次函数,故能量<math>E=T+V</math>也为守恒量。这样我们就得到对称陀螺的三个一次积分(守恒量)。 | ||
| + | <math>\begin{align}\left\{\begin{array}{r} | ||
| + | I_1\sin^2\theta\dot\varphi+I_3\cos\theta\left(\cos\theta\dot\varphi+\dot\psi\right)=c_1,\\ | ||
| + | I_3\left(\cos\theta\dot\varphi+\dot\psi\right)=c_2,\\ | ||
| + | \frac{1}{2}I_1\left(\dot\theta^2+\sin^2\theta\dot\varphi^2\right)+\frac{1}{2}I_3\left(\cos\theta\dot\varphi+\dot\psi\right)^2+mgl\cos\theta=c_3, | ||
| + | \end{array}\right.\end{align}</math> | ||
| + | </li> | ||
| + | <li> C.B.柯凡律夫斯卡亚(C.B.Kovaleski)情况:<math>I_1=I_2=2I_3</math>,重心在惯量椭球赤道面上。</li> | ||
| + | </ol> | ||
| + | </li> | ||
| + | <li> 拉莫尔进动:匀强磁场中,转动带电物体的角动量随时间的变化满足 | ||
| + | <br/><math>\begin{align}\frac{{\rm d}\boldsymbol{J}}{{\rm d}t}=-\frac{e\boldsymbol{B}}{2m}\times\boldsymbol{J}\end{align}</math><br/> | ||
| + | 与刚体角动量随时间的变化公式 | ||
| + | <math>\begin{align} \frac{{\rm d}\boldsymbol{J}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{J}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{J}.\end{align}</math> | ||
| + | 比较,可知带电物体的角动量大小不变,以角速度 <math>\boldsymbol{\omega}_l\equiv \frac{e\boldsymbol{B}}{2m}</math> 转动(绕磁场方向转动,类似于陀螺的进动),称为拉莫尔进动。</li> | ||
| + | </ol> | ||
== 转动参考系 == | == 转动参考系 == | ||
| 第232行: | 第392行: | ||
---- | ---- | ||
| − | + | 基本出发点:矢量 <math>\boldsymbol{G}=G_x\boldsymbol{i}+G_y\boldsymbol{j}+G_z\boldsymbol{k}</math>,如果单位矢量 <math>\boldsymbol{i},\boldsymbol{j},\boldsymbol{i}</math> 方向随时间而变化,那么矢量随时间的变化率为 | |
| + | <br/><math>\frac{{\rm d}\boldsymbol{G}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{G},</math><br/> | ||
| + | 上式中 <math>\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}=\dot G_x\boldsymbol{i}+\dot G_y\boldsymbol{j}+\dot G_z\boldsymbol{k}</math>。 | ||
| + | <ol> | ||
| + | <li>平面转动参考系(坐标原点与静止坐标系相同): <math>\begin{align}\left\{\begin{array}{l} | ||
\boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ | \boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ | ||
\boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}-\omega^2\boldsymbol{r}+2\boldsymbol{\omega}\times\boldsymbol{v}^\prime\\ | \boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}-\omega^2\boldsymbol{r}+2\boldsymbol{\omega}\times\boldsymbol{v}^\prime\\ | ||
~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} | ~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} | ||
| − | \end{array}\right.\end{align}</math> | + | \end{array}\right.\end{align}</math></li> |
| − | + | <li>空间转动参考系(坐标原点与静止坐标系相同):<math>\begin{align}\left\{\begin{array}{l} | |
\boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ | \boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ | ||
| − | \boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+\boldsymbol{\omega}(\boldsymbol{\omega}\ | + | \boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+\boldsymbol{\omega}\times(\boldsymbol{\omega}\times\boldsymbol{r})+2\boldsymbol{\omega}\times\boldsymbol{v}^\prime\\ |
~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} | ~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} | ||
| − | \end{array}\right.\end{align}</math> | + | \end{array}\right.\end{align}</math><br/> |
| − | + | </li> | |
| − | + | <li>非惯性系动力学:<math>\boldsymbol{a}_{\rm t}</math> 和 <math>\boldsymbol{a}_{\rm c}</math> 的影响等价于 <math>-m\boldsymbol{a}_{\rm t}</math>(惯性力)和 <math>-m\boldsymbol{a}_{\rm c}</math>(科里奥利力)的作用,即 | |
| − | + | <br/><math>\begin{align}\left\{\begin{array}{ll} | |
| − | + | m\boldsymbol{a}^\prime=\boldsymbol{F}-m\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+m\omega^2\boldsymbol{r}-2m\boldsymbol{\omega}\times\boldsymbol{v}^\prime,&(平面转动参考系)\\ | |
| − | + | m\boldsymbol{a}^\prime=\boldsymbol{F}-m\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+m\omega^2\boldsymbol{R}-2m\boldsymbol{\omega}\times\boldsymbol{v}^\prime,&(空间转动参考系) | |
| − | + | \end{array}\right.\end{align}</math><br/> | |
| − | + | 上式应用了 <math>\boldsymbol{\omega}\times(\boldsymbol{\omega}\times\boldsymbol{r})=(\boldsymbol{\omega}\cdot\boldsymbol{r})\boldsymbol{\omega}-\omega^2\boldsymbol{r}=-\omega^2\boldsymbol{R}</math>。 | |
| − | + | </li> | |
| − | + | <li>应用 | |
| − | + | <ol> | |
| + | <li>地球自转对地表物体运动造成的影响</li> | ||
| + | <li>傅科摆</li> | ||
| + | <li>地漏涡旋方向与地球自转有无关联?</li> | ||
| + | <li>考虑表面完全被水覆盖的行星,自转对行星表面的水波有无影响?对行星尺度的水波有无影响?</li> | ||
| + | <li>木星是巨型气体行星,表面有大红斑。试分析木星自转在大红斑形成和演化过程中的影响?</li></ol></li> | ||
| + | </ol> | ||
| − | === | + | == 分析力学 == |
| + | === 变分法 === | ||
| + | 变分:函数整体的微小变化,<math>f\to f+\delta f</math><br/> | ||
| + | 变分问题例子: | ||
| + | * 最速降线问题: <math>\displaystyle I=\int_{x_A}^{x_B}\frac{\sqrt{1+y^{\prime 2}}}{\sqrt{2gy}}{\rm d}x</math> | ||
| + | * 最小曲面问题:<math>\displaystyle I=\int_{x_A}^{x_B}y\sqrt{1+y^{\prime 2}}{\rm d}x </math> | ||
| + | * 等周问题,等等。<br/> | ||
| + | 变分问题:给定关于函数 <math>y(x)</math> 的定积分 <math>\displaystyle I=\int_{x_{A}}^{x_{B}} f(y,y^\prime){\rm d}x</math>,求解函数形式变化时积分的极小值。 | ||
| + | 类比于普通函数极小值的求法,<math>I</math> 取极小值的条件为变分值为 0,即 <math>y\to y+\delta y</math>,有 <math>\delta I=0</math>。由此可以得到<span style="color: blue">'''变分极值满足的条件——欧拉-拉格朗日方程'''</span>: | ||
| + | <br/><math>\displaystyle \frac{\rm d}{{\rm d}x}\frac{\partial f}{\partial y^\prime}+\frac{\partial f}{\partial y}=0.</math><br/> | ||
| + | 这里有一些[[变分计算例子]]可供练习。 | ||
| − | + | === 拉格朗日方程 === | |
| + | <ol> | ||
| − | + | <li><span style="color: blue">'''哈密顿原理'''</span>:两点之间粒子的运动轨迹是作用量取极值的轨迹,即<math>\delta S=0</math><br/> | |
| − | + | 上式中作用量 <math>\begin{align}S\equiv\int_{t_1}^{t_2}L(x,\dot x,t){\rm d}t=0\end{align}</math>,拉格朗日函数<math>L=T-V</math>.<br/> | |
| − | + | 根据哈密顿原理,<br/> | |
| + | <math>\begin{align} | ||
| + | \delta S=&\int_{t_A}^{t_B} \delta L(x,\dot x,t){\rm d}t\\ | ||
| + | =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\delta\dot x\right]{\rm d}t\\ | ||
| + | =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\frac{\rm d}{{\rm d}t}\delta x\right]{\rm d}t\\ | ||
| + | =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\delta x\right)-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\delta x\right]{\rm d}t\\ | ||
| + | =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\right]\delta x{\rm d}t+\left.\left(\frac{\partial L}{\partial\dot x}\delta x\right)\right|_{t_A}^{t_B}\\ | ||
| + | =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\right]\delta x{\rm d}t | ||
| + | \end{align}</math><br/> | ||
| + | 因为<math>\delta x</math>是任意满足<math>\delta x(t_A)=\delta x(t_B)=0</math>的光滑函数,因此他与另一函数的积分值为零意味着这个函数处处为0,因此我们得到欧拉-拉格朗日方程 | ||
| + | <br/><math>\begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial \dot x}\right)-\frac{\partial L}{\partial x}=0.\end{align}</math><br/></li> | ||
| − | = | + | <li><span style="color: blue">'''拉格朗日方程'''</span>:如果系统运动由 <math>s</math> 个独立的广义坐标 <math> q_1,\ldots,q_s</math> 描述,则拉格朗日函数为<math> L(q_1,\ldots,q_s;\dot q_1,\ldots,\dot q_s;t)</math>,应用哈密顿原理,根据广义坐标的线性无关性,得到 <math>s</math> 个拉格朗日方程。此为保守系的拉格朗日方程: |
| − | == | + | <br/><math>\begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial q_\alpha}\right)-\frac{\partial L}{\partial q_\alpha}=0,\hspace{4ex}\left(\alpha=1,\ldots,s\right)\end{align}</math><br/> |
| − | + | 上式中广义坐标 <math> q_\alpha</math>、广义速度 <math>\dot q_\alpha</math>。另外广义动量 <math>p_\alpha=\begin{align}\frac{\partial T}{\partial \dot q_\alpha}\end{align}</math>、广义力 <math>\begin{align} Q_\alpha=-\frac{\partial V}{\partial q_\alpha}=\sum_{i=1}^n\boldsymbol{F}_i\cdot\frac{\partial\boldsymbol{r}_i}{\partial q_\alpha}\end{align}</math>。将<math>L=T-V</math>带入保守系的拉格朗日方程,得到基本形式的拉格朗日方程: | |
| − | + | <br/><math>\begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial T}{\partial \dot q_\alpha}\right)-\frac{\partial T}{\partial q_\alpha}=Q_\alpha,~~~~~(\alpha=1,2,\ldots,s)\end{align}</math><br/> | |
| − | # | + | 基本形式的拉格朗日方程可以应用到非保守系。 |
| − | + | </li> | |
| − | + | ||
| − | + | <li>拉格朗日方程的<span style="color: blue">'''运动积分'''</span> | |
| − | + | # 如果 <math>\frac{\partial L}{\partial q_\beta}=0</math>,则<math>q_\beta</math>是系统的循环坐标,对应的广义动量是守恒量即<math>p_\beta\equiv \frac{\partial L}{\partial \dot q_\beta}=C</math> | |
| − | + | # <math>T=T_0+T_2</math>,两项分别是广义速度的零次幂和二次幂。如果拉格朗日函数不显含时间,即 <math>\frac{\partial L}{\partial t}=0</math>,那么我们有能量积分 <math> T_2-T_0+V=h </math>,其中 <math>h</math> 不代表总能量;进一步,如果 <math>T_0=0</math>,则有能量积分 <math>T+V=E</math>,能量守恒。 | |
| − | + | 上式分别代表广义的动量守恒和能量守恒律。</li> | |
| − | + | </ol> | |
| + | |||
| + | === 虚功原理 === | ||
| + | <ol> | ||
| + | <li> <span style="color: blue">'''虚功原理'''</span>力学系统平衡条件为 <math>\begin{align} \delta W=\sum_{i=1}^n \boldsymbol{F_i}\cdot\delta\boldsymbol{r}_i=0\end{align}</math>,亦可表示为 <math> \begin{align} Q_\alpha =0,\hspace{1ex}\left(\alpha=1,\ldots,s\right)\end{align}</math>,其中 <math>s</math> 是系统的自由度数。<br/> | ||
| + | 利用虚功原理求解平衡位置的方法: | ||
| + | # 确定系统的自由度数和广义坐标 <math>q_1,\ldots,q_s</math> | ||
| + | # 写出所有主动力的作用点的位矢 <math>\boldsymbol{r}_i(q_1,\ldots,q_s),~~~(i=1,\ldots,n)</math>,求出用广义坐标 <math>q_1,\ldots,q_s</math> 表示的变分 <math>\begin{align}\delta\boldsymbol{r}_i=\sum_{\alpha=1}^s\frac{{\rm d}\boldsymbol{r}}{{\rm d}q_\alpha}\delta q_\alpha\end{align}</math> | ||
| + | # 将 <math>\delta\boldsymbol{r}_i</math> 的形式代入 <math>\delta W=0</math> 中,合并同类项。广义坐标变分 <math>\delta q_\alpha</math> 前边的系数均为0,得到 <math> s</math> 个方程,从而求出平衡位置的 <math> s</math> 个广义坐标。 | ||
| + | </li> | ||
| + | |||
| + | <li><span style="color: blue">'''拉格朗日未定乘子法(重要)'''</span>:在约束 <math>\begin{align} f_\beta(x_1,\ldots,x_n)=0,(\beta=1,2,\ldots,m)\end{align}</math> 限制下求解具有 <math>n</math> 个自变量的函数 <math>V(x_1,\ldots,x_n)</math> 的极值,等价于求解具有 <math>n+m</math> 个自变量的函数 | ||
| + | <br/><math>\begin{align}\tilde V(x_1,\ldots,x_n;\lambda_1,\ldots,\lambda_m)=V(x_1,\ldots,x_n)+\sum_{\beta=1}^m \lambda_\beta f_\beta(x_1,\ldots,x_n)\end{align}</math><br/> | ||
| + | 的极值。上式中 <math>\lambda_\beta</math> 叫做拉格朗日未定乘子。<math>\tilde V</math> 取极值的必要条件为对所有变量的一阶偏导为0:<br/> | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{l} | ||
| + | \frac{\partial \tilde V}{\partial x_\alpha}=\frac{\partial V}{\partial x_\alpha}+\sum_{\beta=1}^m \lambda_\beta \frac{\partial f_\beta}{\partial x_\alpha}=0,\hspace{3ex}(\alpha=1,\ldots,n,)\\ | ||
| + | \frac{\partial\tilde V}{\partial\lambda_\beta}=f_\beta=0,\hspace{3ex}(\beta=1,\ldots,m) | ||
| + | \end{array}\right.\end{align}</math><br/> | ||
| + | </li> | ||
| + | </ol> | ||
=== 小振动 === | === 小振动 === | ||
| − | + | 力学系统在平衡位置附近做微小振动,运动方程必为简谐振动或若干简谐振动的叠加。 | |
| − | + | <ol> | |
| − | + | <li> 一维情况,平衡位置意味着势函数在 <math>x_0</math> 处有 <math>V^\prime(x_0)=0,~~~V^{\prime\prime}(x_0)>0 </math>。将势函数对小参数 <math>\xi\equiv x-x_0</math> 作泰勒展开,得到势函数的近似形式 <math>V(x)\approx V_0+\frac{1}{2}k\xi^2,~~~(k\equiv V^{\prime\prime}(x_0)>0)</math>,因此运动方程变为 <math> m\ddot \xi+k\xi=0</math>,即简谐振动。</li> | |
| − | \end{array}\right.\end{align}</math> | + | <li> 多维运动的质点,取平衡位置为广义坐标原点和势能零点。在平衡位置附近对势函数作泰勒展开,得到系统动能和势能的表达式 <math>\begin{align}\left\{\begin{array}{l} |
| − | + | T=\frac{1}{2}\sum_{\alpha,\beta=1}^s b_{\alpha\beta} \dot q_\alpha\dot q_\beta,\\ | |
| − | + | V\approx \frac{1}{2}\sum_{\alpha,\beta=1}^s c_{\alpha\beta }q_\alpha q_\beta, | |
| − | + | \end{array}\right.\end{align}</math>, | |
| − | + | 代入拉格朗日方程,得到系统的动力学方程 <math>\begin{align} \sum_{\beta=1}^s \ddot b_{\alpha\beta} \ddot q_\beta+\sum_{\beta=1}^s c_{\alpha\beta}q_\beta=0\end{align} </math>。<br/> | |
| − | + | 上述方程的解是简谐振动的叠加,即 <math>\begin{align} q_\alpha=\sum_{\beta=1}^s d_{\alpha\beta}\cos(\nu_\beta t+\varepsilon_\beta)\end{align}</math> ;通过坐标变换将 <math>V</math> 和 <math>T</math >对角化,解出的独立振动的坐标 <math>\xi_\beta=A_\beta\cos(\nu_\beta t+\varepsilon_\beta)</math> 叫做简正坐标,对应的角频率 <math>\nu_\beta</math>叫做简正频率。</li> | |
| + | <li>简正频率的求解:首先将方程化为如下形式 <math>\begin{align} \ddot q_\alpha=\sum_{\beta=1}^s a_{\alpha\beta} q_\beta\end{align}</math>,即 | ||
| + | <br/><math>\begin{align}\left(\begin{array}{c} \ddot q_1\\ \ddot q_2\\ \vdots\\\ddot q_s\end{array}\right)= | ||
| + | \left(\begin{array}{cccc} | ||
| + | a_{11} & a_{12} &\ldots & a_{1s}\\ | ||
| + | a_{21} & a_{22} &\ldots & a_{2s}\\ | ||
| + | \vdots & \vdots & \ddots & \vdots\\ | ||
| + | a_{s1} & a_{s2} & \ldots & a_{ss} | ||
| + | \end{array}\right) | ||
| + | \left(\begin{array}{c} q_1\\q_2\\\vdots\\q_s\end{array}\right) | ||
| + | \end{align}</math><br/> | ||
| + | 即 <math> \ddot{\boldsymbol{q}}=N\boldsymbol{q} </math>,<math>N</math>为矩阵。上述方程求解的关键,是寻找正交矩阵 <math>M</math> 使得 <math>MNM^T</math> 为对角矩阵。方程两边同时左乘以 <math> M</math>,有 <math>M\ddot{\boldsymbol{q}}=MN\boldsymbol{q}=MNM^{-1}M\boldsymbol{q} </math>;定义 <math>\boldsymbol{\xi}=M\boldsymbol{q}</math>,则上述方程可以化为<math>\ddot{\boldsymbol{\xi}}=MNM^{T}\boldsymbol{\xi}</math>,即 | ||
| + | <br/><math>\begin{align}\left(\begin{array}{c} \ddot \xi_1\\ \ddot \xi_2\\ \vdots\\\ddot \xi_s\end{array}\right)= | ||
| + | \left(\begin{array}{cccc} | ||
| + | \lambda_1 & 0 &\ldots & 0\\ | ||
| + | 0 & \lambda_2 &\ldots & 0\\ | ||
| + | \vdots & \vdots &\ddots & \vdots\\ | ||
| + | 0 & 0 & \ldots & \lambda_s | ||
| + | \end{array}\right) | ||
| + | \left(\begin{array}{c} \xi_1\\\xi_2\\\vdots\\\xi_s\end{array}\right) | ||
| + | \end{align}</math><br/> | ||
| + | 也即 <math> \ddot \xi_1=\lambda_1 \xi_1,~~~\ddot \xi_2=\lambda_2 \xi_2,\ldots,\ddot \xi_s=\lambda_s \xi_s</math>,方程的解为 <math> \xi_\alpha=A_\alpha\cos(\sqrt{-\lambda_\alpha}t+\epsilon_\alpha) </math> | ||
| + | <br/> | ||
| + | 确定正交矩阵 <math>M</math> ,需要求矩阵 <math>N</math> 的特征值和特征矢。特征值通过求解以下特征多项式得到: | ||
| + | <br/><math>\begin{align} | ||
| + | \left|\begin{array}{cccc} | ||
| + | a_{11}-\lambda & a_{12} &\ldots & a_{1s}\\ | ||
| + | a_{21} & a_{22}-\lambda &\ldots & a_{2s}\\ | ||
| + | \vdots & \vdots & \ddots & \vdots\\ | ||
| + | a_{s1} & a_{s2} & \ldots & a_{ss}-\lambda | ||
| + | \end{array}\right|=0 | ||
| + | \end{align}</math><br/> | ||
| + | 将求得的 <math>\lambda_1,\lambda_2,\ldots,\lambda_s</math> 代入 <math> N\boldsymbol{v}_\alpha=\lambda_\alpha\boldsymbol{v}_\alpha </math>,同时利用归一化条件 <math>\boldsymbol{v}_\alpha\cdot\boldsymbol{v}_{\beta}=\delta_{\alpha\beta} </math>,可以求出 <math> s</math> 个正交归一本征矢,其中 <math> \begin{align} \boldsymbol{v}_\alpha = \left( \begin{array}{c} v_{\alpha 1}\\ v_{\alpha 2}\\ \vdots\\ v_{\alpha s}\end{array}\right)\end{align}</math>。每个本征矢占一行,组成的矩阵即为变换矩阵 <math>M</math> ,即 | ||
| + | <br/><math>\begin{align} | ||
| + | M=\left(\begin{array}{c} | ||
| + | \boldsymbol{v}_1\\ | ||
| + | \boldsymbol{v}_2\\ | ||
| + | \vdots\\ | ||
| + | \boldsymbol{v}_s\\ | ||
| + | \end{array}\right) | ||
| + | = | ||
| + | \left(\begin{array}{cccc} | ||
| + | v_{11} & v_{12} &\ldots & v_{1s}\\ | ||
| + | v_{21} & v_{22} &\ldots & v_{2s}\\ | ||
| + | \vdots & \vdots & \ddots & \vdots\\ | ||
| + | v_{s1} & v_{s2} & \ldots & v_{ss} | ||
| + | \end{array}\right) | ||
| + | \end{align}</math><br/> | ||
| + | 最后,根据定义 <math>\boldsymbol{\xi}=M\boldsymbol{q}</math>,有 <math>\boldsymbol{q}=M^{T}\boldsymbol{\xi}</math>,从而得到方程的解 <math>\begin{align} q_\alpha=\sum_{\beta=1}^s d_{\alpha\beta}\cos(\nu_\beta t+\varepsilon_\beta),~~~~(\alpha=1,2,\ldots,s)\end{align}</math>。<br/> | ||
| + | 另外,根据周衍柏教材分析,方程也可以直接通过本征多项式的代数余子式直接写出,即 <math>\begin{align} q_\beta(t)=\sum_{l=1}^s \Delta_{1\beta}(-\nu_l^2)\cos(\nu_l t+\varepsilon_l)\end{align}</math> | ||
| + | </li> | ||
| + | <li>物理学中大量讨论的是系统在平衡位置附近的微振动,因此均可以应用上述小振动近似,简谐振动<span style="color:blue">'''普适的'''</span>存在于物理学研究的各种系统中。</li> | ||
| + | </ol> | ||
=== 哈密顿方程 === | === 哈密顿方程 === | ||
| − | + | <ol> | |
| − | + | <li> <span style="color: blue">'''勒让德变换'''</span>:<math>f(x)</math> 对 <math>x</math> 的勒让德变换为 <math>\bar f(u)=ux(u)-f\big(x(u)\big),~~~\left(u=\frac{{\rm d} f(x)}{{\rm d}x}\Longrightarrow x=x(u)\right)</math><br/> | |
| − | + | 哈密顿函数:<math>\begin{align} H(p,q,t)=\sum_{i=1}^s p_\alpha\dot q_\alpha-L(q_1,\ldots,q_s;\dot q_1,\ldots,\dot q_s;t)\end{align}</math><br/> | |
| + | <span style="color: blue">'''哈密顿正则方程'''</span>:<math>\begin{align}\left\{\begin{array}{l} | ||
\dot q_\alpha=\frac{\partial H}{\partial p_\alpha},\\ | \dot q_\alpha=\frac{\partial H}{\partial p_\alpha},\\ | ||
\dot p_\alpha=-\frac{\partial H}{\partial q_\alpha}, | \dot p_\alpha=-\frac{\partial H}{\partial q_\alpha}, | ||
| − | \end{array}\right.~~~~(\alpha=1 | + | \end{array}\right.~~~~(\alpha=1,\ldots,s)\end{align}</math> |
| − | + | 式中<math>q_\alpha,p_\alpha</math>叫做正则变量。</li> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | <li> <span style="color: blue">'''泊松括号'''</span>:<math>\begin{align} [A,B]\equiv\sum_{\alpha=1}^s\left(\frac{\partial A}{\partial q_\alpha}\frac{\partial B}{\partial p_\alpha}-\frac{\partial A}{\partial p_\alpha}\frac{\partial B}{\partial q_\alpha}\right)\end{align}</math>。<br/> |
| − | + | 对于依赖于正则变量的函数 <math>\varphi(q_1,\ldots,q_s;p_1,\ldots,p_s;t)</math>,利用正则方程可以将其随时间的变化率表示为 <math>\begin{align}\frac{{\rm d}\varphi}{{\rm d}t}=\frac{\partial \varphi}{\partial t}+[\varphi,H]\end{align}</math><br/> | |
| − | + | 关于运动积分: | |
| − | + | * 如果哈密顿函数不依赖于某个坐标 <math>q_\beta</math>,即 <math>\frac{\partial H}{\partial q_\beta}=0</math>,那么对应的正则动量守恒 <math>p_\beta=c_\beta,</math>; | |
| − | + | * 如果哈密顿函数不显含时间 <math>\frac{\partial H}{\partial t}=0</math>,取 <math>\varphi=H</math>,根据 <math>\frac{{\rm d}\varphi}{{\rm d}t}</math> 的表达式,易见哈密顿函数守恒,即 <math>H=h</math>是守恒量; | |
| − | + | * 对于一般的函数<math>\varphi</math>,如果它不显含时间即<math>\frac{\partial \varphi}{\partial t}=0</math>,且他与哈密顿函数的泊松括号为0即 <math>\left[\varphi, H\right]=0</math>,则此函数也是守恒量 <math>\varphi=C</math> | |
| − | + | * 泊松定理:如果 <math>\varphi</math> 和 <math>\psi</math> 是正则方程的积分,则 <math>[\varphi,\psi]</math> 也是正则方程的积分。</li> | |
| − | + | ||
| − | + | <li> 例:电磁场中的带电粒子,哈密顿函数为 <math>L=\frac{1}{2}mv^2-q\varphi+q\boldsymbol{A}\cdot\boldsymbol{v}</math>,正则动量依定义有 <math>\boldsymbol{p}\equiv\frac{\partial L}{\partial \boldsymbol{v}}=m\boldsymbol{v}+q\boldsymbol{A}</math>,勒让德变换得到哈密顿函数 <math>H=\boldsymbol{p}\cdot\boldsymbol{v}-L=\frac{1}{2}mv^2+q\varphi=\frac{1}{2m}\left(\boldsymbol{p}-q\boldsymbol{A}\right)^2+q\varphi</math>。<br/> | |
| − | + | 注意区分两种动量:普通的<span style="color:blue">'''机械动量为'''</span> <math>m\dot{\boldsymbol{r}}=\boldsymbol{p}-q\boldsymbol{A}</math>,仅与质点的运动方程 <math>\boldsymbol{r}(t)</math> 有关;<span style="color:blue">'''正则动量'''</span>为 <math>\boldsymbol{p}=m\dot{\boldsymbol{r}}+q\boldsymbol{A}</math>,与质点的运动方程 <math>\boldsymbol{r}(t)</math> 和电磁场矢量势 <math>\boldsymbol{A}(\boldsymbol{r},t)</math> 均有关。 | |
| + | </ol> | ||
| + | |||
| + | === 哈密顿方程的一般求解方法:正则变换 & 哈密顿-雅可比理论 === | ||
| + | |||
| + | <ol> | ||
| + | |||
| + | <li> 正则变换:保证哈密顿方程形式不变的坐标变换;<br/> | ||
| + | 正则变换条件为 | ||
| + | <br/><math>\begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}q_\alpha-P_\alpha{\rm d}Q_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_1\end{align}</math> <br/> | ||
| + | 上式也可以变形为 | ||
| + | <br/><math>\begin{align} \sum_{\alpha=1}^s\left(-q_\alpha{\rm d}p_\alpha-P_\alpha{\rm d}Q_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_2,\hspace{3ex}\left(U_2=U_1-\sum_{\alpha=1}^s \left(p_\alpha q_\alpha\right)\right)\end{align}</math> <br/> | ||
| + | <br/><math>\begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}p_\alpha+Q_\alpha{\rm d}P_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_3,\hspace{3ex}\left(U_3=U_1+\sum_{\alpha=1}^s \left(P_\alpha Q_\alpha\right)\right)\end{align}</math> <br/> | ||
| + | 上式中<math>U_2,U_3</math>均为<math>U_1</math>的勒让德变换。<br/> | ||
| + | 如果正则形式和 <math>U</math> 均不显含 <math>t</math>,则正则变换条件变为 | ||
| + | <br/> <math>\begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}p_\alpha-P_\alpha{\rm d}Q_\alpha\right)={\rm d}U\end{align}</math>,且 <math>H^*=H</math>。<br/> | ||
| + | 正则变换的关键在于确保变换后的力学系统含有尽可能多的循环积分。<br/> | ||
| + | 最理想的情况,<math>\begin{align} H^*=H^*(P_1,P_2,\ldots,P_\alpha,t) \end{align}</math>,则方程完全解出:<math>P_\alpha=</math>常数,<math>Q_\alpha=\int\frac{\partial H^*}{\partial P_\alpha}{\rm d}t,~~~(\alpha=1,2,\ldots,s)</math></li> | ||
| + | |||
| + | <li><span style="color: blue">'''哈密顿-雅可比方程'''</span>:选取母函数 <math>S=U</math> 使得变换后的哈密顿函数 <math>H^*=0</math>,则母函数的满足的方程为 <math>\begin{align}\frac{\partial S}{\partial t}+H\left(t;q_1,q_2,\ldots,q_s;\frac{\partial S}{\partial q_1},\frac{\partial S}{\partial q_2},\ldots,\frac{\partial S}{\partial q_s}\right)=0\end{align}</math><br/> | ||
| + | 如果哈密顿函数不显含 <math>t</math> 且约束为稳定的,则 <math>\begin{align}S=-Et+W(q_1,q_2,\ldots,q_s,\alpha_1,\alpha_2,\ldots,\alpha_s,E)+C\end{align}</math>,其中 <math>W</math> 叫做哈密顿-雅可比特性函数。哈密顿-雅可比方程变为 | ||
| + | <br/><math>\begin{align}H\left(q_1,q_2,\ldots,q_s,\frac{\partial W}{\partial q_1},\frac{\partial W}{\partial q_2},\ldots,\frac{\partial W}{\partial q_s}\right)=E,\end{align}</math><br/></li> | ||
| + | |||
| + | <li>分离变量法求解哈密顿-雅可比方程:如果哈密顿函数<math>H</math>对坐标<math>q_\alpha</math>及偏导数<math>\frac{\partial W}{\partial q_\alpha}</math>的依赖可以放到一起,即 | ||
| + | <br/><math>\begin{align}H\left(q_1,\ldots,q_{\alpha-1},q_{\alpha+1},\ldots,q_s;\frac{\partial W}{\partial q_1},\ldots,\frac{\partial W}{\partial q_{\alpha-1}},\frac{\partial W}{\partial q_{\alpha+1}},\ldots,\frac{\partial W}{\partial q_s};\varphi_\alpha\left(q_\alpha,\frac{\partial W}{\partial q_\alpha}\right)\right)=E\end{align}</math><br/> | ||
| + | 则我们可以得到 | ||
| + | <br/><math>\begin{align}\left\{\begin{array}{l} | ||
| + | \varphi_\alpha\left(q_\alpha,\frac{\partial W}{\partial q_\alpha}\right)=c_\alpha,\\ | ||
| + | H\left(q_1,\ldots,q_{\alpha-1},q_{\alpha+1},\ldots,q_s;\frac{\partial W}{\partial q_1},\ldots,\frac{\partial W}{\partial q_{\alpha-1}},\frac{\partial W}{\partial q_{\alpha+1}},\ldots,\frac{\partial W}{\partial q_s};c_\alpha \right)=E | ||
| + | \end{array}\right.\end{align}</math><br/> | ||
| + | <math>c_\alpha</math>是特征值。继续对哈密顿函数的其他变量应用分离变量法,可以依次解出方程。 | ||
| + | </li> | ||
| + | <li> 哈密顿-雅可比方程是经典力学与量子力学的桥梁。薛定谔在建立量子力学的基本方程——哈密顿方程——的时候,就是从哈密顿-雅可比方程出发进行讨论的。详见薛定谔的论文集《Collected papers on wave mechanics》. | ||
| + | </ol> | ||
=== 刘维尔定理 === | === 刘维尔定理 === | ||
| + | 质点的相空间分布函数<math>\rho(q_1,\ldots,q_s,p_1,\ldots,p_s,t)</math>随时间的变化率满足 | ||
| + | <br/><math>\begin{align}\frac{{\rm d}\rho}{{\rm d}t}=\frac{\partial\rho}{\partial t}+\left[\rho,H\right]=0.\end{align}</math><br/> | ||
| − | === | + | === 弯曲空间的拉格朗日方程与广义相对论 === |
| − | ---- | + | <ol> |
| + | |||
| + | <li> 三维欧式空间中曲面和曲线上质点的运动:<br/> | ||
| + | 曲面上,质点位矢参数方程为 <math>\boldsymbol{r}(u,v)</math>,速度为 <math>\boldsymbol{v}=\dot{\boldsymbol{r}}=\boldsymbol{r}_u\dot u+\boldsymbol{r}_v\dot v </math>,动能为 | ||
| + | <br/><math>\begin{align} T=\frac{1}{2}m\boldsymbol{v}\cdot\boldsymbol{v}=\frac{1}{2}m\left[\boldsymbol{r}_u\cdot\boldsymbol{r}_u\dot u^2+2\boldsymbol{r}_u\cdot \boldsymbol{r}_v\dot u\dot v+\boldsymbol{r}_v\cdot \boldsymbol{r}_v\dot v^2\right]=\frac{1}{2}m\sum_{\alpha,\beta=1}^2 g_{ij}\dot q^i \dot q^j,\end{align} </math><br/> | ||
| + | 其中 <math>\begin{align}g_{ij}=\left(\begin{array}{cc} | ||
| + | \boldsymbol{r}_u\cdot \boldsymbol{r}_u & \boldsymbol{r}_u\cdot \boldsymbol{r}_v\\ | ||
| + | \boldsymbol{r}_u\cdot \boldsymbol{r}_v & \boldsymbol{r}_v\cdot \boldsymbol{r}_v | ||
| + | \end{array}\right)\end{align}</math>,是弯曲空间的度规张量;<math>q^1=u,~~~q^2=v</math>,是弯曲空间的坐标。<br/> | ||
| + | 弯曲空间中两矢量的点积定义为 <math>\begin{align}\boldsymbol{A}\cdot\boldsymbol{B}=\sum_{i,j=1}^2 g_{ij}A^i B^j \end{align}</math>,因此动能可以写为 | ||
| + | <br/><math>\begin{align} T=\frac{1}{2}m\dot{\boldsymbol{q}}\cdot\dot{\boldsymbol{q}}=\frac{1}{2}m\sum_{i,j=1}^2 g_{ij}\dot q^i \dot q^j \end{align}</math><br/> | ||
| + | 如果质点除约束力外不受其他外力,则势能 <math>V=0</math>。将拉格朗日函数 <math>L=T</math> 代入拉格朗日方程<math>\begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot q^\alpha}\right)-\frac{\partial L}{\partial q^\alpha}=0\end{align}</math>中,得到运动方程 | ||
| + | <br/><math>\begin{align} | ||
| + | \frac{\rm d}{{\rm d}t}\left(\sum_{j=1}^2 g_{\alpha j}\dot q^j\right)-\frac{1}{2}\sum_{i,j=1}^2\frac{\partial }{\partial q^\alpha}\left(g_{ij}\right)\dot q^i \dot q^j=0,\\ | ||
| + | \sum_{i,j=1}^2\frac{\partial g_{\alpha j}}{\partial q^i}\dot q^i\dot q^j+ \sum_{j=1}^2 g_{\alpha j}\ddot q^j-\frac{1}{2}\sum_{i,j=1}^2\dot q^i\dot q^j\frac{\partial g_{ij}}{\partial q^\alpha}=0,\\ | ||
| + | \frac{1}{2}\sum_{i,j=1}^2\left(\frac{\partial g_{\alpha j}}{\partial q^i}+\frac{\partial g_{\alpha i}}{\partial q^j}\right)\dot q^i\dot q^j+\sum_{j=1}^2g_{\alpha j}\ddot q^j-\frac{1}{2}\sum_{i,j=1}^2\dot q^i\dot q^j\frac{\partial g_{ij}}{\partial q^\alpha}=0,\\ | ||
| + | \frac{1}{2} \sum_{i,j=1}^2\left(\frac{\partial g_{\alpha j}}{\partial q^i}+\frac{\partial g_{\alpha i}}{\partial q^j}-\frac{\partial g_{ij}}{\partial q^\alpha}\right)\dot q^i\dot q^j+\sum_{j=1}^2g_{\alpha j}\ddot q^j=0. | ||
| + | \end{align}</math><br/> | ||
| + | 定义 <math>g_{ij,k}\equiv\frac{\partial g_{ij}}{\partial q^k}</math>,且两边同乘以 <math>g^{\alpha\beta}</math>,上式变为 | ||
| + | <br/><math>\begin{align} | ||
| + | \sum_{i,j,\alpha=1}^2\frac{1}{2}g^{\alpha\beta}\left(g_{\alpha j,i}+ g_{\alpha i,j}- g_{ij,\alpha}\right)\dot q^i\dot q^j+\sum_{j,\alpha=1}^2g^{\alpha\beta}g_{\alpha j}\ddot q^j=0. | ||
| + | \end{align}</math><br/> | ||
| + | 根据联络的定义 <math>\begin{align} | ||
| + | \Gamma^\alpha_{\mu\nu}\equiv\sum_{\beta=1}^2\frac{1}{2}g^{\alpha\beta}(g_{\mu\beta,\nu}+g_{\nu\beta,\mu}-g_{\mu\nu,\beta}), | ||
| + | \end{align}</math> | ||
| + | 以及度规张量的性质 | ||
| + | <math>\begin{align} | ||
| + | \sum_{\nu=1}^2g^{\mu\nu}g_{\nu\rho}=\delta^\mu_\rho. | ||
| + | \end{align}</math> | ||
| + | 上式变为 | ||
| + | <br/><math>\begin{align} | ||
| + | \sum_{i,j=1}^2\Gamma^\beta_{ij}\dot q^i\dot q^j+\ddot q^\beta=0, | ||
| + | \end{align}</math><br/> | ||
| + | 此即广义相对论中的“测地线方程”,是不受主动力的质点约束在平面上作自由运动的质点的运动方程。 | ||
| + | </li> | ||
| + | |||
| + | <li>四维弯曲时空中质点的运动方程:<br> | ||
| + | 广义相对论中,质点在四维弯曲时空中运动,类比于二维曲面上质点运动的讨论,质点动能仍然可以写为 | ||
| + | <br/><math>\begin{align} T=\frac{1}{2}m\dot{\boldsymbol{q}}\cdot\dot{\boldsymbol{q}}=\frac{1}{2}m\sum_{\mu,\nu=1}^4 g_{\mu\nu}\dot q^\mu \dot q^\nu, \end{align}</math><br/> | ||
| + | 上式中度规张量 <math> g_{\mu\nu}</math> 是四维时空的度规张量,根据广义相对论的基本方程,它的取值是由空间物质分布决定的。广义相对论将引力的作用效果等价于时空弯曲,质点在引力场中的运动等价于质点在弯曲时空中的<span style="color:blue">'''自由运动'''</span>,因此物体的运动方程仍为<span style="color:blue">'''测地线方程</span>,即 | ||
| + | <br/><math>\begin{align} | ||
| + | \sum_{\mu,\nu=1}^4\Gamma^\beta_{\mu\nu}\dot q^\mu\dot q^\nu+\ddot q^\beta=0, | ||
| + | \end{align}</math><br/> | ||
| + | |||
| + | </ol> | ||
| + | |||
| + | == 解题常见注意事项 == | ||
| + | <ol> | ||
| + | |||
| + | <li> 一般解题步骤为: | ||
| + | <ol> <li> 想象运动图像 (理解题意、分析受力、应用守恒律)</li> <li> 根据运动三定理(动量定理、角动量定理、动能定理),列动力学方程 </li> <li> 求解方程</li></ol> </li> | ||
| + | |||
| + | <li> 无质量轻杆(或轻绳),如果仅受2个力作用,则两力必然沿杆(或绳)方向;搭在无质量滑轮上的绳子,两端作用力相等。</li> | ||
| + | |||
| + | <li> 质点或刚体在平衡位置附近作的微小振动,必为简谐振动或几个简谐振动的叠加。</li> | ||
| + | |||
| + | <li> 刚体上一点 B 的速度可以用刚体上另一点 A 的速度求出,即 <math> \boldsymbol{v}_B=\boldsymbol{v}_A+\boldsymbol{\omega}\times \boldsymbol{r}_{BA}</math>,其中 <math>\boldsymbol{r}_{BA}\equiv \boldsymbol{r}_B-\boldsymbol{r}_A</math>;刚体动能为 <math>T=\frac{1}{2}mv_c^2+\frac{1}{2}I_c\omega^2=\frac{1}{2}I_o\omega^2</math>,其中 <math>I_c</math> 和 <math>I_o</math> 分别为刚体绕质心和转动瞬心的转动惯量。</li> | ||
| + | |||
| + | <li> 区分<span style="color:blue">'''参考系'''</span>与<span style="color:blue">'''坐标系'''</span> | ||
| + | * 若参照物(参考系)选定,质点的速度 <math>\boldsymbol{v}</math>/角速度矢量 <math>\boldsymbol{J}</math> 的大小和方向完全确定;坐标系仅仅决定了矢量要分解到哪几个方向上(<math>\boldsymbol{i},\boldsymbol{ j},\boldsymbol{ k}</math> 或 <math>\hat{\boldsymbol{e}}_\xi,\hat{\boldsymbol{e}}_\eta,\hat{\boldsymbol{e}}_\zeta</math>)。 | ||
| + | * 静止坐标系:坐标轴相对于参照物(参考系)静止(如笛卡尔系),速度表示为 <math> \boldsymbol{v}=\dot{\boldsymbol{r}}=\dot x\hat{\boldsymbol{e}}_\xi+\dot y\hat{\boldsymbol{e}}_\eta+\dot z\hat{\boldsymbol{e}}_\zeta </math>; | ||
| + | * 转动坐标系:坐标轴相对于参照物(参考系)有相对转动(如极坐标系、自然坐标系等),速度为 <math> \boldsymbol{v}=\dot{\boldsymbol{r}}=\dot x\boldsymbol{i}+\dot y\boldsymbol{j}+\dot z\boldsymbol{k}+\boldsymbol{\omega}\times \boldsymbol{r} </math>,简写为 <math> \boldsymbol{v}=\boldsymbol{v}^*+\boldsymbol{\omega}\times\boldsymbol{r}</math>,其中 <math>\boldsymbol{\omega}</math> 为三个坐标轴(坐标系)的转动角速度。 | ||
| + | * 平动参考系中角速度相同,转动参考系中角速度不同;转动坐标系中角速度相同。 | ||
| + | * 刚体运动一般选取地面参考系 + 转动坐标系。转动坐标系 <math>o{\rm -}xyz</math> 固定在刚体上,是静止坐标系 <math>o^\prime{\rm -}\xi\eta\zeta</math> 经过三个欧拉角的转动得到的。刚体角速度可以在两个坐标系中分别表出: <math>\boldsymbol{\omega}=\omega_\xi \hat{\boldsymbol{e}}_\xi+\omega_\eta\hat{\boldsymbol{e}}_\eta+\omega_\zeta\hat{\boldsymbol{e}}_\zeta=\omega_x \boldsymbol{i}+\omega_y \boldsymbol{j}+\omega_z \boldsymbol{k}</math>.</li> | ||
| − | + | <li></li> | |
| − | + | </ol> | |
| − | + | ||
2021年6月9日 (三) 17:02的最后版本
参考书籍:
- 朗道,栗弗席兹,《力学(第3版)》(英文影印版),世界图书出版公司
- 朗道十卷本理论物理教程之首。从分析力学讲起,高屋建瓴,推理严密,内容精炼(170页)。可供仔细研读,若感觉难度太高可结合鞠国兴《朗道力学解读》。
- Goldstein et al.,《经典力学(第3版)》(英文影印版),高等教育出版社
- 美国普遍采用的理论力学教材,内容丰富,数学推导详尽,有大量习题。内容略多(约630页)。可供选择性阅读,与教材互补。中译本为第2版,内容更加简练,比第3版缺少“混沌”一章。
- Arnold,《经典力学的数学方法》(英文影印版),世界图书出版公司
- 经典名著,内容有深度,数学要求略高。可供查阅。
- 秦敢、向守平,《力学与理论力学(下册)》,科学出版社
- 中国科学技术大学的经典教材,以分析力学为主,内容精炼(前四章150页),从易到难,适合于中国学生学习使用。
目录
质点力学
质点运动学
- 运动学变量:坐标 $ \begin{align}\boldsymbol{r}\end{align} $,速度 $ \boldsymbol{v}=\dot{\boldsymbol{r}} $,加速度 $ \boldsymbol{a}=\dot{\boldsymbol{v}}=\ddot{\boldsymbol{r}} $,动量 $ \boldsymbol{p}=m\boldsymbol{v} $,角动量 $ \boldsymbol{J}=\boldsymbol{r}\times\boldsymbol{p} $
- 三种坐标系中运动学变量的具体形式(注意坐标轴方向是否随时间变化)
- 笛卡尔坐标系 $ \begin{align}\left\{\begin{array}{l} \boldsymbol{r}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k},\\ \boldsymbol{v}=\dot x\boldsymbol{i}+\dot y\boldsymbol{j}+\dot z\boldsymbol{k},\\ \boldsymbol{a}=\ddot x\boldsymbol{i}+\ddot y\boldsymbol{j}+\ddot z\boldsymbol{k}, \end{array}\right.\end{align} $
- 平面极坐标系 $ \begin{align}\left\{\begin{array}{l} \boldsymbol{r}=r\boldsymbol{i},\\ \boldsymbol{v}=\dot r\boldsymbol{i}+r\dot \theta\boldsymbol{j},\\ \boldsymbol{a}=(\ddot r-r\dot\theta^2)\boldsymbol{i}+\frac{1}{r}\frac{\rm d}{{\rm d}t}(r^2\dot\theta)\boldsymbol{j}, \end{array}\right. \hspace{7ex} \left\{\begin{array}{l} \frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\dot\theta \boldsymbol{j},\\ \frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\dot\theta \boldsymbol{i},\end{array} \right. \end{align} $
- 自然坐标系 $ \begin{align}\left\{\begin{array}{l} \boldsymbol{v}=\dot s\boldsymbol{i},\\ \boldsymbol{a}=\dot v\boldsymbol{i}+\frac{v^2}{\rho}\boldsymbol{j}=a_{\rm t}\boldsymbol{i}+a_{\rm n}\boldsymbol{j}, \end{array}\right. \hspace{7ex} \left\{\begin{array}{l} \frac{{\rm d}\boldsymbol{i}}{{\rm d}t}=\frac{v}{\rho} \boldsymbol{j},\\ \frac{{\rm d}\boldsymbol{j}}{{\rm d}t}=-\frac{v}{\rho} \boldsymbol{i},\end{array} \right. \end{align} \hspace{7ex} \rho=\left|\frac{{\rm d}s}{{\rm d}\theta}\right|=\left|\frac{y^{\prime\prime}}{\left(1+y^\prime\right)^{3/2}}\right|^{-1} $
- 坐标轴随时间变化,则矢量对时间的导数为$ \begin{align} \frac{{\rm d}\boldsymbol{G}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{G},~~~~~~~\left(\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}=\dot G_x\hat i+\dot G_y\hat j+\dot G_z\hat k\right) \end{align} $
质点运动定律
- 牛顿三定律
- 质点不受其他物体作用 $ \Longrightarrow {\it p}= $ 常数
- $ \boldsymbol{F}=m\boldsymbol{a} $
- $ \boldsymbol{F}_{12}=-\boldsymbol{F}_{21},\boldsymbol{r}_{12}\times\boldsymbol{F}_{12}=0 $
- 质点运动微分方程:
- 自由粒子运动微分方程: $ m\ddot{\boldsymbol{r}}=\boldsymbol{F}(\boldsymbol{r},\dot{\boldsymbol{r}},t) $。
分量形式为:
笛卡尔系 平面极坐标系 自然坐标系 $ \begin{align}\left\{\begin{array}{l} m\ddot{x}=F_x(x,y,z;\dot x,\dot y,\dot z;t)\\ m\ddot{y}=F_y(x,y,z;\dot x,\dot y,\dot z;t)\\ m\ddot{z}=F_z(x,y,z;\dot x,\dot y,\dot z;t) \end{array}\right.\end{align} $ $ \begin{align}\left\{\begin{array}{l} m(\ddot r-r{\dot\theta}^2)=F_r(r,\theta;\dot r,\dot\theta;t),\\ m(r\ddot\theta +2\dot r \dot\theta)=F_\theta(r,\theta;\dot r,\dot\theta;t),\\ \end{array}\right.\end{align} $
$ \begin{align}\left\{\begin{array}{l} m\dot v=F_{\rm t},\\ m\frac{v^2}{\rho}=F_{\rm n},\\ 0=F_{\rm b}. \end{array}\right.\end{align} $
- 非自由粒子运动微分方程:$ \begin{align}\left\{\begin{array}{l}m\ddot{\boldsymbol{r}}=\boldsymbol{F}(\boldsymbol{r},\dot{\boldsymbol{r}},t)+\boldsymbol{R},\\ \varphi(\boldsymbol{r})=0~~~(约束方程)\end{array}\right.\end{align} $
分量形式(将$ \boldsymbol{F}\to \boldsymbol{F}+\boldsymbol{R} $) 自然坐标系:$ \begin{align}\left\{\begin{array}{l} m\dot v=F_{\rm t},\\ m\frac{v^2}{\rho}=F_{\rm n}+R_{\rm n},\\ 0=F_{\rm b}+R_{\rm b},\\ \varphi(\boldsymbol{r})=0. \end{array}\right.\end{align} $
- 自由粒子运动微分方程: $ m\ddot{\boldsymbol{r}}=\boldsymbol{F}(\boldsymbol{r},\dot{\boldsymbol{r}},t) $。
分量形式为:
- 求解质点运动微分方程的求解方法:(1)数值解法(差分法,适用于线性/非线性、一阶/二阶/高阶、常微分/偏微分等各种方程);(2)解析法.
以一维运动为例,运动方程为 $ m\ddot x=F(x,\dot x,t) $- 如果 $ F=F(t) $,两边直接积分,解为 $ m (v-v_0)=\int_{t_0}^t F(t){\rm d}t $
- 如果 $ F=F(x) $,则将加速度变形为 $ \ddot x=\frac{1}{2}\frac{{\rm d}\dot x^2}{{\rm d}x} $,解为 $ \frac{m}{2}(v^2-v_0^2)=\int_{x_0}^x F(x){\rm d}x $
- 如果 $ F=F(v) $,根据 $ \ddot x=\dot v $,变为一阶方程 $ m\dot v=F(v) $,解为 $ \int_{v_0}^v\frac{{\rm d}v}{F(v)}=t-t_0 $
- 如果 $ F=g(x)h(v) $,根据上边加速度的表示式 $ \ddot x=v\frac{{\rm d}v}{{\rm d}x} $,得到 $ mv\frac{{\rm d}v}{{\rm d}x}=g(x)h(v) $,为可分离变量的一阶微分方程,解为 $ \int_{v_0}^{v} \frac{v{\rm d}v}{h(v)}=\int_{x_0}^x g(x){\rm d}x $
- 如果 $ F=h(v)f(t) $,根据 $ \ddot x=\dot v $,解为 $ \int_{v_0}^v\frac{{\rm d}v}{h(v)}=\int_{t_0}^t f(t){\rm d}t $
质点运动定理
- 保守力:如果 $ \boldsymbol{F} $ 做功与路径无关,只依赖于出发点和终点坐标,则 $ \boldsymbol{F} $ 叫保守力。
保守力的四个等效条件:- 从 A 到 B 点的曲线积分 $ \int_A^B \boldsymbol{F}\cdot{\rm d}\boldsymbol{r} $ 仅依赖于端点 A 和 B ,与路径无关.
- 沿封闭路径的曲线积分$ \oint_L\boldsymbol{F}\cdot{\rm d}\boldsymbol{r}=0 $
- 满足 $ \nabla\times \boldsymbol{F}=0 $
- 存在标量函数 $ V(\boldsymbol{r}) $ 满足 $ \boldsymbol{F}=-\nabla V(r) $
保守力:conservative force,原始意义是保持系统能量守恒(conserved)的作用力。(见朗道第 $ \S6 $ 节) - 质点运动定理和守恒定律
运动定理 积分和微分形式 运动守恒律 内容 动量定理 $ \dot{\boldsymbol{p}}=\boldsymbol{F} $ , $ {\rm d}\boldsymbol{p}={\rm d}\boldsymbol{F}{\rm d}t $ 动量守恒定律 $ \boldsymbol{F}=0\Longrightarrow\boldsymbol{p}= $常数 角动量定理 $ \dot{\boldsymbol{J}}=\boldsymbol{M} $ , $ {\rm d}\boldsymbol{J}=\boldsymbol{M}{\rm d}t $ 角动量守恒定律 $ \boldsymbol{M}=0\Longrightarrow \boldsymbol{J}= $常数 动能定理 $ {\rm d}T=\boldsymbol{F}\cdot{\rm d}\boldsymbol{r} $ (动能 $ T\equiv \frac{1}{2}mv^2 $) 机械能守恒定律 $ \boldsymbol{F} $ 为保守力 $ \Longrightarrow E= $常数 (总能量 $ E=T+V $)
有心力
- 质点在有心力场中运动 $ \Longrightarrow $ 角动量守恒($ \boldsymbol{J}=\boldsymbol{C}_1 $)$ \Longrightarrow $ 平面运动
- 有心力必定为保守力,$ \boldsymbol{F}=-\nabla U(r) $,其中 $ U(r) $ 为势能 $ \Longrightarrow $ 机械能守恒 ($ E=T+U(r)=C_2 $)
- 质点在有心力场中的运动等价于一维运动:$ m\ddot r=-\nabla V(r) $$ ~~~~~\left(V(r)=U(r)+\frac{\boldsymbol{J}^2}{2mr^2}\right) $
- 轨道有限的条件:有效势能$ V(r) $存在势阱,能量$ E $小于势阱两边势垒的高度,从而质点能够束缚在势阱中运动。
假设势能取幂函数形式,$ U(r)=cr^\alpha $,根据上述条件有$ V^\prime(r)=0,V^{\prime\prime}(r)>0 $,从而得到轨道有限的必要条件为$ \begin{align}\left\{\begin{array}{ll} c>0,&\alpha>0,\\ c<0,&-2<\alpha<0 \end{array}\right.\end{align} $ - 轨道方程:$ \theta=\int \frac{J/r^2{\rm d}r}{\sqrt{2m(E-V(r))}} $;质点在有心力场中运动的轨道封闭的条件:$ \Delta\theta=2\int_{r_{\rm min}}^{r_{\rm max}}\frac{J/r^2{\rm d}r}{\sqrt{2m(E-V(r))}}=\pi \times $有理数
- 圆形轨道的稳定性:从等效一维运动的角度讨论,稳定性意味着粒子束缚在一个势阱中运动。因此稳定性条件与前边的有限性条件相同。
- 万有引力(平方反比引力)作用下运动方程的解:$ r=\frac{p}{1+e\cos\theta}.\hspace{3ex}\left(p=\frac{J^2}{mk^2},e=\sqrt{1+\frac{2EJ^2}{mk^4}}\right) $
- 平方反比斥力:$ \alpha $ 粒子的散射,运动方程的解为 $ r=\frac{p}{e\cos\theta-1}.\hspace{3ex}\left(p=\frac{J^2}{mk^2},e=\sqrt{1+\frac{2EJ^2}{mk^4}}\right) $.
- 扩展(SRT和毕业论文候选)
- 双恒星系统中行星的轨道?居住在行星上的人的历法会如何发展?
常用数学公式
- $ \begin{align} \int\frac{{\rm d}x}{1+x^2}&=\arctan x+C,& \int\frac{{\rm d}x}{\sqrt{1+x^2}}&={\rm arcsinh}\, x+C,\\ \int\frac{{\rm d}x}{1-x^2}&={\rm arctanh}\,x+C,& \int\frac{{\rm d}x}{\sqrt{1-x^2}}&=\arcsin x+C. \end{align} $
- 二阶常系数齐次线性微分方程 $ \ddot x+p\dot x+q x=0 $,解的形式取决于特征方程 $ r^2+pr+q=0 $ 解的情况。
$ \begin{align}x(t)=\left\{\begin{array}{ll} C_1 e^{r_1 t}+C_2 e^{r_2 t},& (2~个不同实根~ r_1\neq r_2)\\ \left(C_1+C_2t\right)e^{rt},& (2重实根~ r_1=r_2\equiv r)\\ e^{\alpha t}\left(C_1\cos\beta t+C_2\sin\beta t\right),&(2~个共轭复根~ r_{1,2}=\alpha\pm i\beta) \end{array}\right.\end{align} $ - 二阶常系数非齐次线性微分方程 $ \ddot x+p\dot x+q x=f(t) $,通解为 $ x=x^*+X $,其中 $ X $ 是对应的齐次方程即当 $ f(t)=0 $ 的时候方程的通解,而 $ x^* $ 是非齐次方程的特解。当 $ f(t)=e^{ct}P_n(t) $ 时($ P_n(t) $ 为 $ t $ 的$ n $ 次多项式,$ c $ 为复数),特解 $ x^* $ 有简单的形式。
取 $ f(t)=e^{\lambda t}\left(P_n(t)\cos\omega t+P_l(t)\sin\omega t\right) $,则 $ \begin{align}x^*=\left\{\begin{array}{l@{~~~~~}l} e^{\lambda t}\left(Q_m(t)\cos\omega t+R_m(t)\sin\omega t\right),&\left(\lambda+i\omega\text{不是特征方程}r^2+pr+q=0\text{的根}\right)\\ te^{\lambda t}\left(Q_m(t)\cos\omega t+R_m(t)\sin\omega t\right),&\left(\lambda+i\omega\text{是特征方程}r^2+pr+q=0\text{的根}\right) \end{array}\right.\end{align} $ 上式中 $ Q_m(t)=a_0+a_1 t+\ldots +a_m t^m,~~~R_m(t)=b_0+b_1 t+\ldots+b_m t^m $,其中 $ m={\rm max}(l,n) $。将 $ Q_m(t),~R_m(t) $ 的形式代回原非齐次方程,让对应项的系数相等从而解出 $ a_1,a_2,\ldots,a_m,b_1,b_2,\ldots,b_m $。这样方程的通解 $ x=x^*+X $ 就完全解出。 - 一阶微分方程
$ \begin{align}\begin{array}{|l|@{~~~}l|@{~~~}l|}\hline \text{方程类型} & \text{方程形式} & \text{方程通解}\\\hline \text{可分离变量} & y^\prime=g(x)h(y) & \int\frac{{\rm d}y}{h(y)}=\int g(x){\rm d}x+C\\\hline \text{齐次微分方程} & y^\prime=\varphi\left(\frac{y}{x}\right) & \int\frac{{\rm d}\tilde y}{\varphi(\tilde y)-\tilde y}=\ln x+C,~~~\left(\tilde y\equiv\frac{y}{x}\right)\\\hline \text{线性微分方程} & y^\prime+P(x)+Q(y)=0 & y=e^{-\int P(x){\rm d}x}\left[-\int Q(x)e^{\int P(x){\rm d}x}{\rm d}x+C\right]\\\hline \text{伯努利方程} & y^\prime+P(x)y+Q(y) y^n=0 & \frac{1}{1-n}\tilde y^\prime+P(x)\tilde y+Q(x)=0,~~~(\tilde y=y^{1-n})\\\hline \end{array}\end{align} $
质点组力学
质点组力学框架
- 运动学:
- 质点组总动量:$ \boldsymbol{p}=m\boldsymbol{v}_c+\boldsymbol{0} $
- 质点组总角动量:$ \begin{align} \boldsymbol{J}=\boldsymbol{r}\times m\boldsymbol{v}_c+\boldsymbol{J}^\prime\end{align} $
- 质点组总动能(柯尼希定理):$ \begin{align} T=\frac{1}{2}m\boldsymbol{v}_c^2+T^\prime\end{align} $,即$ \begin{align}\frac{1}{2}\sum_{i=1}^n m_i \dot{\boldsymbol{r}}_i^{2}=\frac{1}{2}m\dot{\boldsymbol{r}}_C^2+\frac{1}{2}\sum_{i=1}^n m_i \dot{\boldsymbol{r}}_i^{\prime 2}\end{align} $,其中 $ \begin{align} m=\sum_{i=1}^n m_i \end{align} $
- 动力学
- 质点组动量定理:$ \begin{align} {\rm d}\boldsymbol{p}=\left(\sum_{i=1}^n \boldsymbol{F}_i^{(\rm e)}\right){\rm d}t \end{align} $
- 质点组角动量定理:$ \begin{align} {\rm d}\boldsymbol{J}=\left(\sum_{i=1}^n \boldsymbol{M}_i^{(\rm e)}\right){\rm d}t \end{align} $
- 质点组动能定理:$ \begin{align} {\rm d}T=\sum_{i=1}^n \boldsymbol{F}_i^{(\rm e)}\cdot {\rm d}\boldsymbol{r}_i+\sum_{i=1}^n \boldsymbol{F}_i^{(\rm i)}\cdot {\rm d}\boldsymbol{r}_i \end{align} $
两体问题
两质点组成的系统,如果合外力为 0 即 $ 0=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_2^{(\rm e)} $,对每个质点分别列运动方程:$ \begin{align}\left\{\begin{array}{l} m_1\ddot{\boldsymbol{r}}_1=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)},\\ m_2\ddot{\boldsymbol{r}}_2=\boldsymbol{F}_2^{(\rm e)}+\boldsymbol{F}_{12}^{(\rm i)}, \end{array}\right.\end{align} $ ,其中 $ \boldsymbol{F}_{21}^{(\rm i)}=-\boldsymbol{F}_{12}^{(\rm i)} $。
- 两式之和为质心运动微分方程:$ \begin{align}m\ddot{\boldsymbol{r}}_c=0,\hspace{2ex}\left(m=m_1+m_2\right)\end{align} $
- 两式分别乘以 $ m_2 $ 和 $ m_1 $,相减得到:$ m_1m_2\left(\ddot{\boldsymbol{r}}_1-\ddot{\boldsymbol{r}}_2\right)=(m_1+m_2)\left(\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)}\right) $,即 $ \mu\ddot{\boldsymbol{r}}=\boldsymbol{F}_1^{(\rm e)}+\boldsymbol{F}_{21}^{(\rm i)} $,其中 $ \boldsymbol{r}\equiv \boldsymbol{r}_1-\boldsymbol{r}_2 $为两质点的相对位矢, $ \mu\equiv \frac{m_1m_2}{m_1+m_2} $ 叫做折合质量。
如果两质点不受外力,且两质点相互作用力仅依赖于距离(是保守力),那么 $ \boldsymbol{F}_{21}^{(\rm i)}=-\nabla U(\boldsymbol{r}) $,$ \big(U(\boldsymbol{r}) $ 为两质点相互作用势能$ \big) $,上式可化为有心力场中的单质点运动问题 $ \begin{align} \mu \ddot{\boldsymbol{r}}=-\nabla U(\boldsymbol{r})\end{align} $。
简言之,不受外力的两质点的运动,可以等价为质心的匀速直线运动与具有折合质量的质点的相对运动的合成,运动方程分别为 $ \begin{align}\left\{\begin{array}{l} m\ddot{\boldsymbol{r}}_c=0,\\ \mu\ddot{\boldsymbol{r}}=-\nabla U(\boldsymbol{r}). \end{array}\right.\end{align} $
变质量物体运动方程
$ \begin{align} \frac{{\rm d}}{{\rm d}t}\left(m\boldsymbol{v}\right)-\dot m \boldsymbol{v}=\boldsymbol{F}.\end{align} $
位力定理
对于满足坐标和动量均取有限值的运动(包括周期性运动),质点组动能的时间平均值等于位力积时间平均值的负值。即
$ \overline{T}=-\frac{1}{2}\overline{\sum_{i=1}^n\boldsymbol{F}_i\cdot\boldsymbol{r}_i} $
如果势能是坐标的 $ n $次函数,即 $ V(\boldsymbol{r})=cr^n $,则 $ \boldsymbol{r}\cdot\nabla V(\boldsymbol{r})=nV(\boldsymbol{r}) $。因此我们得到
$ \overline{T}=\frac{n}{2}\overline{V} $
在统计力学中,位力定理可以导出理想气体状态方程 $ PV=nRT $,也是可以系统地导出非理想气体状态方程;在量子力学中位力定理也有重要应用。更详细的讨论见 位力定理
刚体力学
刚体运动学
- 刚体有6个自由度,可以取为刚体上的一点O的位矢 $ \boldsymbol{r}_O $ 和转动的角度即三个欧拉角 $ \theta,~~\varphi,~~~\psi $。刚体一般运动为参考点O的平动与绕参考点转动的合成。
- 一般取固定在刚体上的三个相互垂直的轴为坐标轴,建立随刚体运动的坐标系$ o-xyz $。(注意:参考系一般选取地面静止系,与坐标系要区分开)
刚体的位置可用欧拉角描述,他们分别为进动角 $ \varphi $、自转角 $ \psi $、章动角 $ \theta $ :
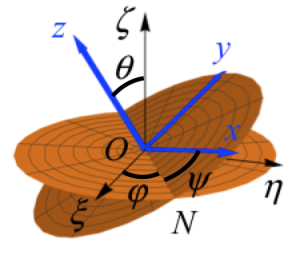
- 欧拉运动学方程:
$ \begin{align}\left\{\begin{array}{l} \omega_x=\dot\varphi\sin\theta\sin\psi+\dot\theta\cos\psi,\\ \omega_y=\dot\varphi\sin\theta\cos\psi-\dot\theta\sin\psi,\\ \omega_z=\dot\varphi\cos\theta+\dot\psi, \end{array}\right.\end{align} $
上式来源于 $ \boldsymbol{\omega}=\dot\varphi\boldsymbol{e}_\zeta+\dot\theta\boldsymbol{e}_{ON}+\dot\psi \boldsymbol{e}_z $,其中 $ \zeta $ 轴和 $ ON $ 轴的方位角和极角分别为 $ \left(\theta,\frac{\pi}{2}-\psi\right) $ 和 $ \left(\frac{\pi}{2},-\psi\right) $ 。刚体转动方向的三个单位矢量在刚体随动系中的表达式为$ \begin{align}\left\{\begin{array}{l} \boldsymbol{e}_\zeta=\sin\theta\sin\psi\boldsymbol{i}+\sin\theta\cos\psi\boldsymbol{j}+\cos\theta\boldsymbol{k},\\ \boldsymbol{e}_{ON}=\cos\psi\boldsymbol{i}-\sin\psi\boldsymbol{j},\\ \boldsymbol{e}_z=\boldsymbol{k}, \end{array}\right.\end{align} $
刚体角速度为矢量,按照普通矢量相加 $ \boldsymbol{\omega}=\boldsymbol{\omega}_1+\boldsymbol{\omega}_2 $ - 刚体转动惯量张量为
$ \begin{align}\hat I=\left(\begin{array}{ccc} \hat I_{xx} & \hat I_{xy} & \hat I_{xz}\\ \hat I_{xy} & \hat I_{yy} & \hat I_{yz}\\ \hat I_{xz} & \hat I_{yz} & \hat I_{zz} \end{array}\right)\end{align} $ 其中惯量张量矩阵元的一般定义式为 $ \begin{align}\hat I_{ij}=\int \left(\boldsymbol{r}^2\delta_{ij}-r_ir_j\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r}\end{align} $,即
$ \begin{align}\hat I_{xx}=\int\left(y^2+z^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ \hat I_{yy}=\int\left(x^2+z^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ \hat I_{zz}=\int\left(x^2+y^2\right)\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\end{align}\hspace{5ex} $ $ \begin{align}\hat I_{xy}=-\int xy\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ \hat I_{yz}=-\int yz\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r},\\ \hat I_{xz}=-\int xz\rho(\boldsymbol{r}){\rm d}^3\boldsymbol{r}.\end{align} $
注意这里的定义与周衍柏教材中的定义的对应:对角元相等,即$ \hat I_{xx}=I_{xx},\hat I_{yy}=I_{yy},\hat I_{zz}=I_{zz} $;非对角元相差一个负号,即$ \hat I_{xy}=-I_{xy},\hat I_{yz}=-I_{yz},\hat I_{xz}=-I_{xz} $ - 作定点运动的刚体,角动量为 $ \boldsymbol{J}=\hat{\boldsymbol{I}}\cdot\boldsymbol{\omega} $,动能为$ T=\frac{1}{2}\boldsymbol{\omega}\cdot\boldsymbol{\hat I}\cdot\boldsymbol{\omega} $。
在刚体的本体坐标系中,角动量和动能可以写为 $ \begin{align} \left(\begin{array}{l}J_x\\J_y\\J_z\end{array}\right) =\left(\begin{array}{rrr}\hat I_{xx}&\hat I_{xy}&\hat I_{xz}\\\hat I_{yx}&\hat I_{yy}&\hat I_{yz}\\\hat I_{zx}&\hat I_{zy}&\hat I_{zz}\end{array}\right) \left(\begin{array}{l}\omega_x\\\omega_y\\\omega_z\end{array}\right)\end{align} $
$ T=\frac{1}{2}(\hat I_{xx}\omega_x^2+\hat I_{yy}\omega_y^2+\hat I_{zz}\omega_z^2+2\hat I_{xy}\omega_x\omega_y+2\hat I_{yz}\omega_y\omega_z+2\hat I_{xz}\omega_x\omega_z)=\frac{1}{2}I_n\omega^2 $,其中 $ \vec\omega=\omega\hat e_n $,$ I_n\equiv \boldsymbol{n}\cdot\hat{\boldsymbol{I}}\cdot\boldsymbol{n} $ 为刚体对过定点且沿 $ \boldsymbol{n} $ 方向的转轴的转动惯量。
空间转动变换,可以将转动惯量张量 $ \hat{\boldsymbol{I}} $ 对角化,此时的坐标轴为惯量主轴。
惯量主轴的求解:惯量椭球 $ \boldsymbol{r}\cdot\hat{\boldsymbol{A}}\cdot\boldsymbol{r}=1 $ 的三个对称轴。 - 刚体上任意一点的速度:$ \boldsymbol{ v}_A=\boldsymbol{ v}_O+\boldsymbol{\omega}\times\boldsymbol{ r}_{OA} $
- 刚体的动能有两部分组成:质心动能和转动动能,即$ T=\frac{1}{2}m\boldsymbol{v}_c^2+\frac{1}{2}I_n\omega^2 $
刚体动力学
刚体动力学方程包括刚体动量定理、刚体角动量定理(即欧拉动力学方程)和刚体动能定理。
- 刚体动量定理:$ m\ddot{\boldsymbol{r}}_c=\boldsymbol{F} $,刚体质心运动由刚体受到的合外力决定。
- 刚体角动量定理:$ \dot{\boldsymbol{J}}=\boldsymbol{M} $,其中角动量 $ \boldsymbol{J}=\hat{\boldsymbol{A}}\cdot\boldsymbol{\omega} $。为简化计算,欧拉采用了两重简化方式
- 采用固定在刚体上的坐标系,则转动惯量张量 $ {\rm d}\hat{\boldsymbol{A}}/{\rm d}t=0 $,角速度 $ \boldsymbol{\omega}=\omega_x\boldsymbol{i}+\omega_y\boldsymbol{j}+\omega_z\boldsymbol{k} $,其中坐标轴的单位矢量随时间变化,满足
$ \begin{align}\frac{{\rm d}^*\boldsymbol{J}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{J}=\boldsymbol{M}.\end{align} $- 取$ o-xyz $的坐标轴为刚体的惯量主轴,则惯量张量为对角矩阵即$ \begin{align}\hat{\boldsymbol{A}}=\left(\begin{array}{ccc} I_1 & 0 & 0\\ 0 & I_2 & 0\\ 0 & 0 & I_3 \end{array}\right)\end{align} $
$ \begin{align}\left\{\begin{array}{l} I_1\dot\omega_x+(I_3-I_2)\omega_y\omega_z=M_x,\\ I_2\dot\omega_y+(I_1-I_3)\omega_z\omega_x=M_y,\\ I_3\dot\omega_z+(I_2-I_1)\omega_x\omega_y=M_z. \end{array}\right.\end{align} $ - 刚体动能定理:$ \begin{align}{\rm d}T=\sum_{i=1}^n\boldsymbol{F}^{(\rm e)}_i\cdot{\rm d}\boldsymbol{r}_i\end{align} $,其中刚体动能为$ T=\frac{1}{2}mv_c^2+\frac{1}{2}I_n\omega^2 $
刚体运动分类
- 刚体平动:欧拉角为常数,角速度$ \boldsymbol{\omega}=0 $。自由度数 $ s=3 $,取为刚体质心位矢。
- 刚体定轴转动:刚体上一点固定,且角速度仅沿一个方向。自由度数 $ s=1 $,取为自转角。
把角速度方向取为z方向,则$ \omega_x=\omega_y=0 $,角动量简化为 $ \boldsymbol{J}=I_{xz}\omega_z\boldsymbol{i}+I_{yz}\omega_z\boldsymbol{j}+I_{zz}\omega_z\boldsymbol{k} $,刚体的角动量定理变为
$ \begin{align}\left\{\begin{array}{r} I_{xz}\dot\omega_z-I_{yz}\omega_z^2=M_x,\\ I_{yz}\dot\omega_z+I_{xz}\omega_z^2=M_y,\\ I_{zz}\dot\omega_z=M_z, \end{array}\right.\end{align} $
最后一式是动力学方程,前两式可以用来求解对刚体转轴的约束力。 - 刚体平面平行运动:刚体上一点做平面运动,且刚体角速度垂直于这个平面。自由度数 $ s=3 $,取为刚体上一点在平面内的位矢和刚体的转动角度。
刚体的角动量定理同上,动量定理只涉及x和y方向,即$ \begin{align}\left\{\begin{array}{l} m\ddot{\boldsymbol{x}}_c=\boldsymbol{F}_x,\\ m\ddot{\boldsymbol{y}}_c=\boldsymbol{F}_y, \end{array}\right.\end{align} $
平面平行运动的刚体必有转动瞬心$ O $。转动瞬心可以简化刚体的运动描述- 刚体的总动能可以写为 $ T=\frac{1}{2}I_O\omega^2 $ ,$ I_O $ 是绕瞬心的转动惯量
- 刚体上一点的速度可以写为 $ \boldsymbol{v}=\boldsymbol{\omega}\times\boldsymbol{r}^\prime $,$ \boldsymbol{r}^\prime $ 是该点相对于转动瞬心的相对位矢。
- 已知刚体上两点速度,如果速度方向不同,则瞬心为两速度垂线的交点;
- 已知刚体上一点速度和刚体角动量,则瞬心位于过该点且垂直于速度的直线上,且与该点的距离为$ \frac{v}{\omega} $;
- 已知两点的速度,速度方向相同,且过一点速度的垂线穿过第二点,则可以建立相似三角形确定速度;
- 如果两点速度平行且速度的垂涎穿过两点,则刚体的转动瞬心在无穷远处。
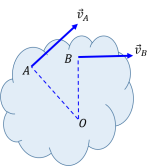
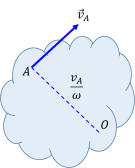 $ \hspace{3ex} $
$ \hspace{3ex} $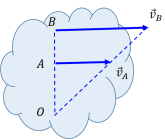
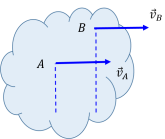
转动瞬心划过的轨迹,在地面静止系中叫做空间极迹;在刚体静止系中叫做本体极迹。 - 刚体定点转动:刚体上有一固定点O,角速度无限制。自由度数 $ s=3 $,取为刚体的三个欧拉角。
刚体定点运动的动力学方程完整的欧拉动力学方程。
重刚体:主动力仅有重力的刚体。有解析解的重刚体有三种:- 欧拉-潘索情况:外力通过固定点O,$ \boldsymbol{M}=0 $,刚体在惯性下运动。欧拉动力学方程简化为
$ \begin{align}\left\{\begin{array}{l} I_1\dot\omega_x-(I_2-I_3)\omega_y\omega_z=0,\\ I_2\dot\omega_y-(I_3-I_1)\omega_z\omega_x=0,\\ I_3\dot\omega_z-(I_1-I_2)\omega_x\omega_y=0. \end{array}\right.\end{align} $
根据上述方程,可以求出$ \omega_x,\omega_y,\omega_z $;再利用欧拉动力学方程,求出欧拉角随时间变化的方程$ \theta(t),\varphi(t),\psi(t) $。这样运动方程就完全解出。
当$ I_1=I_2 $的特殊情况下(比如地球),运动方程可以得到简化。
潘索引入了几何方法,可以比较简便的说明一般情况下($ I_1\neq I_2\neq I_3 $)刚体的运动图像。 - 拉格朗日-泊松情况(对称陀螺):重力作用点不过固定点O,但有$ I_1=I_2 $。欧拉动力学方程化简为
$ \begin{align}\left\{\begin{array}{l} I_1\dot\omega_x-(I_1-I_3)\omega_y\omega_z=mgl\sin\theta\cos\psi,\\ I_1\dot\omega_y+(I_3-I_1)\omega_z\omega_x=mgl\sin\theta\sin\psi,\\ I_3\dot\omega_z=0. \end{array}\right.\end{align} $
根据欧拉运动学方程,易得对称陀螺的拉格朗日函数 $ \begin{align}L=\frac{1}{2}I_1\left(\dot\theta^2+\sin^2\theta\dot\varphi^2\right)+\frac{1}{2}I_3\left(\cos\theta\dot\varphi+\dot\psi\right)^2-mgl\cos\theta\end{align} $。因为拉格朗日函数对$ \varphi $和$ \psi $没有依赖,因此对应的广义动量为一次积分(守恒量);同时,因为动量是广义速度的二次函数,故能量$ E=T+V $也为守恒量。这样我们就得到对称陀螺的三个一次积分(守恒量)。 $ \begin{align}\left\{\begin{array}{r} I_1\sin^2\theta\dot\varphi+I_3\cos\theta\left(\cos\theta\dot\varphi+\dot\psi\right)=c_1,\\ I_3\left(\cos\theta\dot\varphi+\dot\psi\right)=c_2,\\ \frac{1}{2}I_1\left(\dot\theta^2+\sin^2\theta\dot\varphi^2\right)+\frac{1}{2}I_3\left(\cos\theta\dot\varphi+\dot\psi\right)^2+mgl\cos\theta=c_3, \end{array}\right.\end{align} $ - C.B.柯凡律夫斯卡亚(C.B.Kovaleski)情况:$ I_1=I_2=2I_3 $,重心在惯量椭球赤道面上。
- 欧拉-潘索情况:外力通过固定点O,$ \boldsymbol{M}=0 $,刚体在惯性下运动。欧拉动力学方程简化为
- 拉莫尔进动:匀强磁场中,转动带电物体的角动量随时间的变化满足
$ \begin{align}\frac{{\rm d}\boldsymbol{J}}{{\rm d}t}=-\frac{e\boldsymbol{B}}{2m}\times\boldsymbol{J}\end{align} $
与刚体角动量随时间的变化公式 $ \begin{align} \frac{{\rm d}\boldsymbol{J}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{J}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{J}.\end{align} $ 比较,可知带电物体的角动量大小不变,以角速度 $ \boldsymbol{\omega}_l\equiv \frac{e\boldsymbol{B}}{2m} $ 转动(绕磁场方向转动,类似于陀螺的进动),称为拉莫尔进动。
转动参考系
知识要点
基本出发点:矢量 $ \boldsymbol{G}=G_x\boldsymbol{i}+G_y\boldsymbol{j}+G_z\boldsymbol{k} $,如果单位矢量 $ \boldsymbol{i},\boldsymbol{j},\boldsymbol{i} $ 方向随时间而变化,那么矢量随时间的变化率为
$ \frac{{\rm d}\boldsymbol{G}}{{\rm d}t}=\frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}+\boldsymbol{\omega}\times\boldsymbol{G}, $
上式中 $ \frac{{\rm d}^*\boldsymbol{G}}{{\rm d}t}=\dot G_x\boldsymbol{i}+\dot G_y\boldsymbol{j}+\dot G_z\boldsymbol{k} $。
- 平面转动参考系(坐标原点与静止坐标系相同): $ \begin{align}\left\{\begin{array}{l} \boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ \boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}-\omega^2\boldsymbol{r}+2\boldsymbol{\omega}\times\boldsymbol{v}^\prime\\ ~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} \end{array}\right.\end{align} $
- 空间转动参考系(坐标原点与静止坐标系相同):$ \begin{align}\left\{\begin{array}{l} \boldsymbol{v}=\boldsymbol{v}^\prime+\boldsymbol{\omega}\times\boldsymbol{r},\\ \boldsymbol{a}=\boldsymbol{a}^\prime+\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+\boldsymbol{\omega}\times(\boldsymbol{\omega}\times\boldsymbol{r})+2\boldsymbol{\omega}\times\boldsymbol{v}^\prime\\ ~~=\boldsymbol{a}^\prime+\boldsymbol{a}_{\rm t}+\boldsymbol{a}_{\rm c} \end{array}\right.\end{align} $
- 非惯性系动力学:$ \boldsymbol{a}_{\rm t} $ 和 $ \boldsymbol{a}_{\rm c} $ 的影响等价于 $ -m\boldsymbol{a}_{\rm t} $(惯性力)和 $ -m\boldsymbol{a}_{\rm c} $(科里奥利力)的作用,即
$ \begin{align}\left\{\begin{array}{ll} m\boldsymbol{a}^\prime=\boldsymbol{F}-m\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+m\omega^2\boldsymbol{r}-2m\boldsymbol{\omega}\times\boldsymbol{v}^\prime,&(平面转动参考系)\\ m\boldsymbol{a}^\prime=\boldsymbol{F}-m\dot{\boldsymbol{\omega}}\times\boldsymbol{r}+m\omega^2\boldsymbol{R}-2m\boldsymbol{\omega}\times\boldsymbol{v}^\prime,&(空间转动参考系) \end{array}\right.\end{align} $
上式应用了 $ \boldsymbol{\omega}\times(\boldsymbol{\omega}\times\boldsymbol{r})=(\boldsymbol{\omega}\cdot\boldsymbol{r})\boldsymbol{\omega}-\omega^2\boldsymbol{r}=-\omega^2\boldsymbol{R} $。 - 应用
- 地球自转对地表物体运动造成的影响
- 傅科摆
- 地漏涡旋方向与地球自转有无关联?
- 考虑表面完全被水覆盖的行星,自转对行星表面的水波有无影响?对行星尺度的水波有无影响?
- 木星是巨型气体行星,表面有大红斑。试分析木星自转在大红斑形成和演化过程中的影响?
分析力学
变分法
变分:函数整体的微小变化,$ f\to f+\delta f $
变分问题例子:
- 最速降线问题: $ \displaystyle I=\int_{x_A}^{x_B}\frac{\sqrt{1+y^{\prime 2}}}{\sqrt{2gy}}{\rm d}x $
- 最小曲面问题:$ \displaystyle I=\int_{x_A}^{x_B}y\sqrt{1+y^{\prime 2}}{\rm d}x $
- 等周问题,等等。
变分问题:给定关于函数 $ y(x) $ 的定积分 $ \displaystyle I=\int_{x_{A}}^{x_{B}} f(y,y^\prime){\rm d}x $,求解函数形式变化时积分的极小值。
类比于普通函数极小值的求法,$ I $ 取极小值的条件为变分值为 0,即 $ y\to y+\delta y $,有 $ \delta I=0 $。由此可以得到变分极值满足的条件——欧拉-拉格朗日方程:
$ \displaystyle \frac{\rm d}{{\rm d}x}\frac{\partial f}{\partial y^\prime}+\frac{\partial f}{\partial y}=0. $
这里有一些变分计算例子可供练习。
拉格朗日方程
- 哈密顿原理:两点之间粒子的运动轨迹是作用量取极值的轨迹,即$ \delta S=0 $
上式中作用量 $ \begin{align}S\equiv\int_{t_1}^{t_2}L(x,\dot x,t){\rm d}t=0\end{align} $,拉格朗日函数$ L=T-V $.
根据哈密顿原理,
$ \begin{align} \delta S=&\int_{t_A}^{t_B} \delta L(x,\dot x,t){\rm d}t\\ =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\delta\dot x\right]{\rm d}t\\ =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\frac{\rm d}{{\rm d}t}\delta x\right]{\rm d}t\\ =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}\delta x+\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\delta x\right)-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\delta x\right]{\rm d}t\\ =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\right]\delta x{\rm d}t+\left.\left(\frac{\partial L}{\partial\dot x}\delta x\right)\right|_{t_A}^{t_B}\\ =&\int_{t_A}^{t_B} \left[\frac{\partial L}{\partial x}-\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot x}\right)\right]\delta x{\rm d}t \end{align} $
因为$ \delta x $是任意满足$ \delta x(t_A)=\delta x(t_B)=0 $的光滑函数,因此他与另一函数的积分值为零意味着这个函数处处为0,因此我们得到欧拉-拉格朗日方程
$ \begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial \dot x}\right)-\frac{\partial L}{\partial x}=0.\end{align} $ - 拉格朗日方程:如果系统运动由 $ s $ 个独立的广义坐标 $ q_1,\ldots,q_s $ 描述,则拉格朗日函数为$ L(q_1,\ldots,q_s;\dot q_1,\ldots,\dot q_s;t) $,应用哈密顿原理,根据广义坐标的线性无关性,得到 $ s $ 个拉格朗日方程。此为保守系的拉格朗日方程:
$ \begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial q_\alpha}\right)-\frac{\partial L}{\partial q_\alpha}=0,\hspace{4ex}\left(\alpha=1,\ldots,s\right)\end{align} $
上式中广义坐标 $ q_\alpha $、广义速度 $ \dot q_\alpha $。另外广义动量 $ p_\alpha=\begin{align}\frac{\partial T}{\partial \dot q_\alpha}\end{align} $、广义力 $ \begin{align} Q_\alpha=-\frac{\partial V}{\partial q_\alpha}=\sum_{i=1}^n\boldsymbol{F}_i\cdot\frac{\partial\boldsymbol{r}_i}{\partial q_\alpha}\end{align} $。将$ L=T-V $带入保守系的拉格朗日方程,得到基本形式的拉格朗日方程:
$ \begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial T}{\partial \dot q_\alpha}\right)-\frac{\partial T}{\partial q_\alpha}=Q_\alpha,~~~~~(\alpha=1,2,\ldots,s)\end{align} $
基本形式的拉格朗日方程可以应用到非保守系。 - 拉格朗日方程的运动积分
- 如果 $ \frac{\partial L}{\partial q_\beta}=0 $,则$ q_\beta $是系统的循环坐标,对应的广义动量是守恒量即$ p_\beta\equiv \frac{\partial L}{\partial \dot q_\beta}=C $
- $ T=T_0+T_2 $,两项分别是广义速度的零次幂和二次幂。如果拉格朗日函数不显含时间,即 $ \frac{\partial L}{\partial t}=0 $,那么我们有能量积分 $ T_2-T_0+V=h $,其中 $ h $ 不代表总能量;进一步,如果 $ T_0=0 $,则有能量积分 $ T+V=E $,能量守恒。
虚功原理
- 虚功原理力学系统平衡条件为 $ \begin{align} \delta W=\sum_{i=1}^n \boldsymbol{F_i}\cdot\delta\boldsymbol{r}_i=0\end{align} $,亦可表示为 $ \begin{align} Q_\alpha =0,\hspace{1ex}\left(\alpha=1,\ldots,s\right)\end{align} $,其中 $ s $ 是系统的自由度数。
利用虚功原理求解平衡位置的方法:- 确定系统的自由度数和广义坐标 $ q_1,\ldots,q_s $
- 写出所有主动力的作用点的位矢 $ \boldsymbol{r}_i(q_1,\ldots,q_s),~~~(i=1,\ldots,n) $,求出用广义坐标 $ q_1,\ldots,q_s $ 表示的变分 $ \begin{align}\delta\boldsymbol{r}_i=\sum_{\alpha=1}^s\frac{{\rm d}\boldsymbol{r}}{{\rm d}q_\alpha}\delta q_\alpha\end{align} $
- 将 $ \delta\boldsymbol{r}_i $ 的形式代入 $ \delta W=0 $ 中,合并同类项。广义坐标变分 $ \delta q_\alpha $ 前边的系数均为0,得到 $ s $ 个方程,从而求出平衡位置的 $ s $ 个广义坐标。
- 拉格朗日未定乘子法(重要):在约束 $ \begin{align} f_\beta(x_1,\ldots,x_n)=0,(\beta=1,2,\ldots,m)\end{align} $ 限制下求解具有 $ n $ 个自变量的函数 $ V(x_1,\ldots,x_n) $ 的极值,等价于求解具有 $ n+m $ 个自变量的函数
$ \begin{align}\tilde V(x_1,\ldots,x_n;\lambda_1,\ldots,\lambda_m)=V(x_1,\ldots,x_n)+\sum_{\beta=1}^m \lambda_\beta f_\beta(x_1,\ldots,x_n)\end{align} $
的极值。上式中 $ \lambda_\beta $ 叫做拉格朗日未定乘子。$ \tilde V $ 取极值的必要条件为对所有变量的一阶偏导为0:
$ \begin{align}\left\{\begin{array}{l} \frac{\partial \tilde V}{\partial x_\alpha}=\frac{\partial V}{\partial x_\alpha}+\sum_{\beta=1}^m \lambda_\beta \frac{\partial f_\beta}{\partial x_\alpha}=0,\hspace{3ex}(\alpha=1,\ldots,n,)\\ \frac{\partial\tilde V}{\partial\lambda_\beta}=f_\beta=0,\hspace{3ex}(\beta=1,\ldots,m) \end{array}\right.\end{align} $
小振动
力学系统在平衡位置附近做微小振动,运动方程必为简谐振动或若干简谐振动的叠加。
- 一维情况,平衡位置意味着势函数在 $ x_0 $ 处有 $ V^\prime(x_0)=0,~~~V^{\prime\prime}(x_0)>0 $。将势函数对小参数 $ \xi\equiv x-x_0 $ 作泰勒展开,得到势函数的近似形式 $ V(x)\approx V_0+\frac{1}{2}k\xi^2,~~~(k\equiv V^{\prime\prime}(x_0)>0) $,因此运动方程变为 $ m\ddot \xi+k\xi=0 $,即简谐振动。
- 多维运动的质点,取平衡位置为广义坐标原点和势能零点。在平衡位置附近对势函数作泰勒展开,得到系统动能和势能的表达式 $ \begin{align}\left\{\begin{array}{l} T=\frac{1}{2}\sum_{\alpha,\beta=1}^s b_{\alpha\beta} \dot q_\alpha\dot q_\beta,\\ V\approx \frac{1}{2}\sum_{\alpha,\beta=1}^s c_{\alpha\beta }q_\alpha q_\beta, \end{array}\right.\end{align} $,
代入拉格朗日方程,得到系统的动力学方程 $ \begin{align} \sum_{\beta=1}^s \ddot b_{\alpha\beta} \ddot q_\beta+\sum_{\beta=1}^s c_{\alpha\beta}q_\beta=0\end{align} $。
上述方程的解是简谐振动的叠加,即 $ \begin{align} q_\alpha=\sum_{\beta=1}^s d_{\alpha\beta}\cos(\nu_\beta t+\varepsilon_\beta)\end{align} $ ;通过坐标变换将 $ V $ 和 $ T $对角化,解出的独立振动的坐标 $ \xi_\beta=A_\beta\cos(\nu_\beta t+\varepsilon_\beta) $ 叫做简正坐标,对应的角频率 $ \nu_\beta $叫做简正频率。 - 简正频率的求解:首先将方程化为如下形式 $ \begin{align} \ddot q_\alpha=\sum_{\beta=1}^s a_{\alpha\beta} q_\beta\end{align} $,即
$ \begin{align}\left(\begin{array}{c} \ddot q_1\\ \ddot q_2\\ \vdots\\\ddot q_s\end{array}\right)= \left(\begin{array}{cccc} a_{11} & a_{12} &\ldots & a_{1s}\\ a_{21} & a_{22} &\ldots & a_{2s}\\ \vdots & \vdots & \ddots & \vdots\\ a_{s1} & a_{s2} & \ldots & a_{ss} \end{array}\right) \left(\begin{array}{c} q_1\\q_2\\\vdots\\q_s\end{array}\right) \end{align} $
即 $ \ddot{\boldsymbol{q}}=N\boldsymbol{q} $,$ N $为矩阵。上述方程求解的关键,是寻找正交矩阵 $ M $ 使得 $ MNM^T $ 为对角矩阵。方程两边同时左乘以 $ M $,有 $ M\ddot{\boldsymbol{q}}=MN\boldsymbol{q}=MNM^{-1}M\boldsymbol{q} $;定义 $ \boldsymbol{\xi}=M\boldsymbol{q} $,则上述方程可以化为$ \ddot{\boldsymbol{\xi}}=MNM^{T}\boldsymbol{\xi} $,即
$ \begin{align}\left(\begin{array}{c} \ddot \xi_1\\ \ddot \xi_2\\ \vdots\\\ddot \xi_s\end{array}\right)= \left(\begin{array}{cccc} \lambda_1 & 0 &\ldots & 0\\ 0 & \lambda_2 &\ldots & 0\\ \vdots & \vdots &\ddots & \vdots\\ 0 & 0 & \ldots & \lambda_s \end{array}\right) \left(\begin{array}{c} \xi_1\\\xi_2\\\vdots\\\xi_s\end{array}\right) \end{align} $
也即 $ \ddot \xi_1=\lambda_1 \xi_1,~~~\ddot \xi_2=\lambda_2 \xi_2,\ldots,\ddot \xi_s=\lambda_s \xi_s $,方程的解为 $ \xi_\alpha=A_\alpha\cos(\sqrt{-\lambda_\alpha}t+\epsilon_\alpha) $
确定正交矩阵 $ M $ ,需要求矩阵 $ N $ 的特征值和特征矢。特征值通过求解以下特征多项式得到:
$ \begin{align} \left|\begin{array}{cccc} a_{11}-\lambda & a_{12} &\ldots & a_{1s}\\ a_{21} & a_{22}-\lambda &\ldots & a_{2s}\\ \vdots & \vdots & \ddots & \vdots\\ a_{s1} & a_{s2} & \ldots & a_{ss}-\lambda \end{array}\right|=0 \end{align} $
将求得的 $ \lambda_1,\lambda_2,\ldots,\lambda_s $ 代入 $ N\boldsymbol{v}_\alpha=\lambda_\alpha\boldsymbol{v}_\alpha $,同时利用归一化条件 $ \boldsymbol{v}_\alpha\cdot\boldsymbol{v}_{\beta}=\delta_{\alpha\beta} $,可以求出 $ s $ 个正交归一本征矢,其中 $ \begin{align} \boldsymbol{v}_\alpha = \left( \begin{array}{c} v_{\alpha 1}\\ v_{\alpha 2}\\ \vdots\\ v_{\alpha s}\end{array}\right)\end{align} $。每个本征矢占一行,组成的矩阵即为变换矩阵 $ M $ ,即
$ \begin{align} M=\left(\begin{array}{c} \boldsymbol{v}_1\\ \boldsymbol{v}_2\\ \vdots\\ \boldsymbol{v}_s\\ \end{array}\right) = \left(\begin{array}{cccc} v_{11} & v_{12} &\ldots & v_{1s}\\ v_{21} & v_{22} &\ldots & v_{2s}\\ \vdots & \vdots & \ddots & \vdots\\ v_{s1} & v_{s2} & \ldots & v_{ss} \end{array}\right) \end{align} $
最后,根据定义 $ \boldsymbol{\xi}=M\boldsymbol{q} $,有 $ \boldsymbol{q}=M^{T}\boldsymbol{\xi} $,从而得到方程的解 $ \begin{align} q_\alpha=\sum_{\beta=1}^s d_{\alpha\beta}\cos(\nu_\beta t+\varepsilon_\beta),~~~~(\alpha=1,2,\ldots,s)\end{align} $。
另外,根据周衍柏教材分析,方程也可以直接通过本征多项式的代数余子式直接写出,即 $ \begin{align} q_\beta(t)=\sum_{l=1}^s \Delta_{1\beta}(-\nu_l^2)\cos(\nu_l t+\varepsilon_l)\end{align} $ - 物理学中大量讨论的是系统在平衡位置附近的微振动,因此均可以应用上述小振动近似,简谐振动普适的存在于物理学研究的各种系统中。
哈密顿方程
- 勒让德变换:$ f(x) $ 对 $ x $ 的勒让德变换为 $ \bar f(u)=ux(u)-f\big(x(u)\big),~~~\left(u=\frac{{\rm d} f(x)}{{\rm d}x}\Longrightarrow x=x(u)\right) $
哈密顿函数:$ \begin{align} H(p,q,t)=\sum_{i=1}^s p_\alpha\dot q_\alpha-L(q_1,\ldots,q_s;\dot q_1,\ldots,\dot q_s;t)\end{align} $
哈密顿正则方程:$ \begin{align}\left\{\begin{array}{l} \dot q_\alpha=\frac{\partial H}{\partial p_\alpha},\\ \dot p_\alpha=-\frac{\partial H}{\partial q_\alpha}, \end{array}\right.~~~~(\alpha=1,\ldots,s)\end{align} $ 式中$ q_\alpha,p_\alpha $叫做正则变量。 - 泊松括号:$ \begin{align} [A,B]\equiv\sum_{\alpha=1}^s\left(\frac{\partial A}{\partial q_\alpha}\frac{\partial B}{\partial p_\alpha}-\frac{\partial A}{\partial p_\alpha}\frac{\partial B}{\partial q_\alpha}\right)\end{align} $。
对于依赖于正则变量的函数 $ \varphi(q_1,\ldots,q_s;p_1,\ldots,p_s;t) $,利用正则方程可以将其随时间的变化率表示为 $ \begin{align}\frac{{\rm d}\varphi}{{\rm d}t}=\frac{\partial \varphi}{\partial t}+[\varphi,H]\end{align} $
关于运动积分:- 如果哈密顿函数不依赖于某个坐标 $ q_\beta $,即 $ \frac{\partial H}{\partial q_\beta}=0 $,那么对应的正则动量守恒 $ p_\beta=c_\beta, $;
- 如果哈密顿函数不显含时间 $ \frac{\partial H}{\partial t}=0 $,取 $ \varphi=H $,根据 $ \frac{{\rm d}\varphi}{{\rm d}t} $ 的表达式,易见哈密顿函数守恒,即 $ H=h $是守恒量;
- 对于一般的函数$ \varphi $,如果它不显含时间即$ \frac{\partial \varphi}{\partial t}=0 $,且他与哈密顿函数的泊松括号为0即 $ \left[\varphi, H\right]=0 $,则此函数也是守恒量 $ \varphi=C $
- 泊松定理:如果 $ \varphi $ 和 $ \psi $ 是正则方程的积分,则 $ [\varphi,\psi] $ 也是正则方程的积分。
- 例:电磁场中的带电粒子,哈密顿函数为 $ L=\frac{1}{2}mv^2-q\varphi+q\boldsymbol{A}\cdot\boldsymbol{v} $,正则动量依定义有 $ \boldsymbol{p}\equiv\frac{\partial L}{\partial \boldsymbol{v}}=m\boldsymbol{v}+q\boldsymbol{A} $,勒让德变换得到哈密顿函数 $ H=\boldsymbol{p}\cdot\boldsymbol{v}-L=\frac{1}{2}mv^2+q\varphi=\frac{1}{2m}\left(\boldsymbol{p}-q\boldsymbol{A}\right)^2+q\varphi $。
注意区分两种动量:普通的机械动量为 $ m\dot{\boldsymbol{r}}=\boldsymbol{p}-q\boldsymbol{A} $,仅与质点的运动方程 $ \boldsymbol{r}(t) $ 有关;正则动量为 $ \boldsymbol{p}=m\dot{\boldsymbol{r}}+q\boldsymbol{A} $,与质点的运动方程 $ \boldsymbol{r}(t) $ 和电磁场矢量势 $ \boldsymbol{A}(\boldsymbol{r},t) $ 均有关。
哈密顿方程的一般求解方法:正则变换 & 哈密顿-雅可比理论
- 正则变换:保证哈密顿方程形式不变的坐标变换;
正则变换条件为
$ \begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}q_\alpha-P_\alpha{\rm d}Q_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_1\end{align} $
上式也可以变形为
$ \begin{align} \sum_{\alpha=1}^s\left(-q_\alpha{\rm d}p_\alpha-P_\alpha{\rm d}Q_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_2,\hspace{3ex}\left(U_2=U_1-\sum_{\alpha=1}^s \left(p_\alpha q_\alpha\right)\right)\end{align} $
$ \begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}p_\alpha+Q_\alpha{\rm d}P_\alpha\right)+(H^*-H){\rm d}t={\rm d}U_3,\hspace{3ex}\left(U_3=U_1+\sum_{\alpha=1}^s \left(P_\alpha Q_\alpha\right)\right)\end{align} $
上式中$ U_2,U_3 $均为$ U_1 $的勒让德变换。
如果正则形式和 $ U $ 均不显含 $ t $,则正则变换条件变为
$ \begin{align} \sum_{\alpha=1}^s\left(p_\alpha{\rm d}p_\alpha-P_\alpha{\rm d}Q_\alpha\right)={\rm d}U\end{align} $,且 $ H^*=H $。
正则变换的关键在于确保变换后的力学系统含有尽可能多的循环积分。
最理想的情况,$ \begin{align} H^*=H^*(P_1,P_2,\ldots,P_\alpha,t) \end{align} $,则方程完全解出:$ P_\alpha= $常数,$ Q_\alpha=\int\frac{\partial H^*}{\partial P_\alpha}{\rm d}t,~~~(\alpha=1,2,\ldots,s) $ - 哈密顿-雅可比方程:选取母函数 $ S=U $ 使得变换后的哈密顿函数 $ H^*=0 $,则母函数的满足的方程为 $ \begin{align}\frac{\partial S}{\partial t}+H\left(t;q_1,q_2,\ldots,q_s;\frac{\partial S}{\partial q_1},\frac{\partial S}{\partial q_2},\ldots,\frac{\partial S}{\partial q_s}\right)=0\end{align} $
如果哈密顿函数不显含 $ t $ 且约束为稳定的,则 $ \begin{align}S=-Et+W(q_1,q_2,\ldots,q_s,\alpha_1,\alpha_2,\ldots,\alpha_s,E)+C\end{align} $,其中 $ W $ 叫做哈密顿-雅可比特性函数。哈密顿-雅可比方程变为
$ \begin{align}H\left(q_1,q_2,\ldots,q_s,\frac{\partial W}{\partial q_1},\frac{\partial W}{\partial q_2},\ldots,\frac{\partial W}{\partial q_s}\right)=E,\end{align} $ - 分离变量法求解哈密顿-雅可比方程:如果哈密顿函数$ H $对坐标$ q_\alpha $及偏导数$ \frac{\partial W}{\partial q_\alpha} $的依赖可以放到一起,即
$ \begin{align}H\left(q_1,\ldots,q_{\alpha-1},q_{\alpha+1},\ldots,q_s;\frac{\partial W}{\partial q_1},\ldots,\frac{\partial W}{\partial q_{\alpha-1}},\frac{\partial W}{\partial q_{\alpha+1}},\ldots,\frac{\partial W}{\partial q_s};\varphi_\alpha\left(q_\alpha,\frac{\partial W}{\partial q_\alpha}\right)\right)=E\end{align} $
则我们可以得到
$ \begin{align}\left\{\begin{array}{l} \varphi_\alpha\left(q_\alpha,\frac{\partial W}{\partial q_\alpha}\right)=c_\alpha,\\ H\left(q_1,\ldots,q_{\alpha-1},q_{\alpha+1},\ldots,q_s;\frac{\partial W}{\partial q_1},\ldots,\frac{\partial W}{\partial q_{\alpha-1}},\frac{\partial W}{\partial q_{\alpha+1}},\ldots,\frac{\partial W}{\partial q_s};c_\alpha \right)=E \end{array}\right.\end{align} $
$ c_\alpha $是特征值。继续对哈密顿函数的其他变量应用分离变量法,可以依次解出方程。 - 哈密顿-雅可比方程是经典力学与量子力学的桥梁。薛定谔在建立量子力学的基本方程——哈密顿方程——的时候,就是从哈密顿-雅可比方程出发进行讨论的。详见薛定谔的论文集《Collected papers on wave mechanics》.
刘维尔定理
质点的相空间分布函数$ \rho(q_1,\ldots,q_s,p_1,\ldots,p_s,t) $随时间的变化率满足
$ \begin{align}\frac{{\rm d}\rho}{{\rm d}t}=\frac{\partial\rho}{\partial t}+\left[\rho,H\right]=0.\end{align} $
弯曲空间的拉格朗日方程与广义相对论
- 三维欧式空间中曲面和曲线上质点的运动:
曲面上,质点位矢参数方程为 $ \boldsymbol{r}(u,v) $,速度为 $ \boldsymbol{v}=\dot{\boldsymbol{r}}=\boldsymbol{r}_u\dot u+\boldsymbol{r}_v\dot v $,动能为
$ \begin{align} T=\frac{1}{2}m\boldsymbol{v}\cdot\boldsymbol{v}=\frac{1}{2}m\left[\boldsymbol{r}_u\cdot\boldsymbol{r}_u\dot u^2+2\boldsymbol{r}_u\cdot \boldsymbol{r}_v\dot u\dot v+\boldsymbol{r}_v\cdot \boldsymbol{r}_v\dot v^2\right]=\frac{1}{2}m\sum_{\alpha,\beta=1}^2 g_{ij}\dot q^i \dot q^j,\end{align} $
其中 $ \begin{align}g_{ij}=\left(\begin{array}{cc} \boldsymbol{r}_u\cdot \boldsymbol{r}_u & \boldsymbol{r}_u\cdot \boldsymbol{r}_v\\ \boldsymbol{r}_u\cdot \boldsymbol{r}_v & \boldsymbol{r}_v\cdot \boldsymbol{r}_v \end{array}\right)\end{align} $,是弯曲空间的度规张量;$ q^1=u,~~~q^2=v $,是弯曲空间的坐标。
弯曲空间中两矢量的点积定义为 $ \begin{align}\boldsymbol{A}\cdot\boldsymbol{B}=\sum_{i,j=1}^2 g_{ij}A^i B^j \end{align} $,因此动能可以写为
$ \begin{align} T=\frac{1}{2}m\dot{\boldsymbol{q}}\cdot\dot{\boldsymbol{q}}=\frac{1}{2}m\sum_{i,j=1}^2 g_{ij}\dot q^i \dot q^j \end{align} $
如果质点除约束力外不受其他外力,则势能 $ V=0 $。将拉格朗日函数 $ L=T $ 代入拉格朗日方程$ \begin{align}\frac{\rm d}{{\rm d}t}\left(\frac{\partial L}{\partial\dot q^\alpha}\right)-\frac{\partial L}{\partial q^\alpha}=0\end{align} $中,得到运动方程
$ \begin{align} \frac{\rm d}{{\rm d}t}\left(\sum_{j=1}^2 g_{\alpha j}\dot q^j\right)-\frac{1}{2}\sum_{i,j=1}^2\frac{\partial }{\partial q^\alpha}\left(g_{ij}\right)\dot q^i \dot q^j=0,\\ \sum_{i,j=1}^2\frac{\partial g_{\alpha j}}{\partial q^i}\dot q^i\dot q^j+ \sum_{j=1}^2 g_{\alpha j}\ddot q^j-\frac{1}{2}\sum_{i,j=1}^2\dot q^i\dot q^j\frac{\partial g_{ij}}{\partial q^\alpha}=0,\\ \frac{1}{2}\sum_{i,j=1}^2\left(\frac{\partial g_{\alpha j}}{\partial q^i}+\frac{\partial g_{\alpha i}}{\partial q^j}\right)\dot q^i\dot q^j+\sum_{j=1}^2g_{\alpha j}\ddot q^j-\frac{1}{2}\sum_{i,j=1}^2\dot q^i\dot q^j\frac{\partial g_{ij}}{\partial q^\alpha}=0,\\ \frac{1}{2} \sum_{i,j=1}^2\left(\frac{\partial g_{\alpha j}}{\partial q^i}+\frac{\partial g_{\alpha i}}{\partial q^j}-\frac{\partial g_{ij}}{\partial q^\alpha}\right)\dot q^i\dot q^j+\sum_{j=1}^2g_{\alpha j}\ddot q^j=0. \end{align} $
定义 $ g_{ij,k}\equiv\frac{\partial g_{ij}}{\partial q^k} $,且两边同乘以 $ g^{\alpha\beta} $,上式变为
$ \begin{align} \sum_{i,j,\alpha=1}^2\frac{1}{2}g^{\alpha\beta}\left(g_{\alpha j,i}+ g_{\alpha i,j}- g_{ij,\alpha}\right)\dot q^i\dot q^j+\sum_{j,\alpha=1}^2g^{\alpha\beta}g_{\alpha j}\ddot q^j=0. \end{align} $
根据联络的定义 $ \begin{align} \Gamma^\alpha_{\mu\nu}\equiv\sum_{\beta=1}^2\frac{1}{2}g^{\alpha\beta}(g_{\mu\beta,\nu}+g_{\nu\beta,\mu}-g_{\mu\nu,\beta}), \end{align} $ 以及度规张量的性质 $ \begin{align} \sum_{\nu=1}^2g^{\mu\nu}g_{\nu\rho}=\delta^\mu_\rho. \end{align} $ 上式变为
$ \begin{align} \sum_{i,j=1}^2\Gamma^\beta_{ij}\dot q^i\dot q^j+\ddot q^\beta=0, \end{align} $
此即广义相对论中的“测地线方程”,是不受主动力的质点约束在平面上作自由运动的质点的运动方程。 - 四维弯曲时空中质点的运动方程:
广义相对论中,质点在四维弯曲时空中运动,类比于二维曲面上质点运动的讨论,质点动能仍然可以写为
$ \begin{align} T=\frac{1}{2}m\dot{\boldsymbol{q}}\cdot\dot{\boldsymbol{q}}=\frac{1}{2}m\sum_{\mu,\nu=1}^4 g_{\mu\nu}\dot q^\mu \dot q^\nu, \end{align} $
上式中度规张量 $ g_{\mu\nu} $ 是四维时空的度规张量,根据广义相对论的基本方程,它的取值是由空间物质分布决定的。广义相对论将引力的作用效果等价于时空弯曲,质点在引力场中的运动等价于质点在弯曲时空中的自由运动,因此物体的运动方程仍为测地线方程,即
$ \begin{align} \sum_{\mu,\nu=1}^4\Gamma^\beta_{\mu\nu}\dot q^\mu\dot q^\nu+\ddot q^\beta=0, \end{align} $
解题常见注意事项
- 一般解题步骤为:
- 想象运动图像 (理解题意、分析受力、应用守恒律)
- 根据运动三定理(动量定理、角动量定理、动能定理),列动力学方程
- 求解方程
- 无质量轻杆(或轻绳),如果仅受2个力作用,则两力必然沿杆(或绳)方向;搭在无质量滑轮上的绳子,两端作用力相等。
- 质点或刚体在平衡位置附近作的微小振动,必为简谐振动或几个简谐振动的叠加。
- 刚体上一点 B 的速度可以用刚体上另一点 A 的速度求出,即 $ \boldsymbol{v}_B=\boldsymbol{v}_A+\boldsymbol{\omega}\times \boldsymbol{r}_{BA} $,其中 $ \boldsymbol{r}_{BA}\equiv \boldsymbol{r}_B-\boldsymbol{r}_A $;刚体动能为 $ T=\frac{1}{2}mv_c^2+\frac{1}{2}I_c\omega^2=\frac{1}{2}I_o\omega^2 $,其中 $ I_c $ 和 $ I_o $ 分别为刚体绕质心和转动瞬心的转动惯量。
- 区分参考系与坐标系
- 若参照物(参考系)选定,质点的速度 $ \boldsymbol{v} $/角速度矢量 $ \boldsymbol{J} $ 的大小和方向完全确定;坐标系仅仅决定了矢量要分解到哪几个方向上($ \boldsymbol{i},\boldsymbol{ j},\boldsymbol{ k} $ 或 $ \hat{\boldsymbol{e}}_\xi,\hat{\boldsymbol{e}}_\eta,\hat{\boldsymbol{e}}_\zeta $)。
- 静止坐标系:坐标轴相对于参照物(参考系)静止(如笛卡尔系),速度表示为 $ \boldsymbol{v}=\dot{\boldsymbol{r}}=\dot x\hat{\boldsymbol{e}}_\xi+\dot y\hat{\boldsymbol{e}}_\eta+\dot z\hat{\boldsymbol{e}}_\zeta $;
- 转动坐标系:坐标轴相对于参照物(参考系)有相对转动(如极坐标系、自然坐标系等),速度为 $ \boldsymbol{v}=\dot{\boldsymbol{r}}=\dot x\boldsymbol{i}+\dot y\boldsymbol{j}+\dot z\boldsymbol{k}+\boldsymbol{\omega}\times \boldsymbol{r} $,简写为 $ \boldsymbol{v}=\boldsymbol{v}^*+\boldsymbol{\omega}\times\boldsymbol{r} $,其中 $ \boldsymbol{\omega} $ 为三个坐标轴(坐标系)的转动角速度。
- 平动参考系中角速度相同,转动参考系中角速度不同;转动坐标系中角速度相同。
- 刚体运动一般选取地面参考系 + 转动坐标系。转动坐标系 $ o{\rm -}xyz $ 固定在刚体上,是静止坐标系 $ o^\prime{\rm -}\xi\eta\zeta $ 经过三个欧拉角的转动得到的。刚体角速度可以在两个坐标系中分别表出: $ \boldsymbol{\omega}=\omega_\xi \hat{\boldsymbol{e}}_\xi+\omega_\eta\hat{\boldsymbol{e}}_\eta+\omega_\zeta\hat{\boldsymbol{e}}_\zeta=\omega_x \boldsymbol{i}+\omega_y \boldsymbol{j}+\omega_z \boldsymbol{k} $.