“核子结构”的版本间的差异
(→部分子分布函数) |
(→其他) |
||
| (未显示同一用户的15个中间版本) | |||
| 第18行: | 第18行: | ||
== 部分子分布函数 == | == 部分子分布函数 == | ||
| − | 描述质子性质的物理量为部分子分布函数,他们给出了质子内某种部分子的数密度。光锥动量定义为<math>p^\pm\equiv \frac{1}{\sqrt{2}}(p^0\pm p^z)</math>,假定质子沿z方向运动,则质子的四动量为<math>\begin{align}p^\mu=\left(p^+,\frac{M^2}{2p^+},\vec 0_\perp\right)\end{align} | + | 描述质子性质的物理量为部分子分布函数,他们给出了质子内某种部分子的数密度。光锥动量定义为<math>p^\pm\equiv \frac{1}{\sqrt{2}}(p^0\pm p^z)</math>,假定质子沿z方向运动,则质子的四动量为<math>\begin{align}p^\mu=\left(p^+,\frac{M^2}{2p^+},\vec 0_\perp\right)\end{align}</math>。 |
质子的'''夸克分布函数'''定义为 | 质子的'''夸克分布函数'''定义为 | ||
| 第25行: | 第25行: | ||
f_q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\left\langle p\left|\bar\psi_q(0){\cal L}(0,\xi^-)\gamma^+\psi_q(\xi^-)\right|p\right\rangle, | f_q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\left\langle p\left|\bar\psi_q(0){\cal L}(0,\xi^-)\gamma^+\psi_q(\xi^-)\right|p\right\rangle, | ||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
表示质子内动量分数为x、味道为q的夸克的数密度。上式中<math>\displaystyle\langle p|\ldots|p\rangle\equiv \frac{1}{2}\sum_s\langle p,s|\ldots|p,s\rangle</math>, 出现的<math>{\cal L}</math>为规范链,它的存在确保<math>f_q(x)</math>为规范不变的物理观测量。规范链的定义为 | 表示质子内动量分数为x、味道为q的夸克的数密度。上式中<math>\displaystyle\langle p|\ldots|p\rangle\equiv \frac{1}{2}\sum_s\langle p,s|\ldots|p,s\rangle</math>, 出现的<math>{\cal L}</math>为规范链,它的存在确保<math>f_q(x)</math>为规范不变的物理观测量。规范链的定义为 | ||
| 第34行: | 第32行: | ||
\end{align}</math> | \end{align}</math> | ||
| − | 上式中<math>{\cal P}</math>为路径变序算子,它对几个算符乘积的作用效果为:将路径上更靠近终点的算子移动到左边,靠近起始点的算子移动到右边;a为色指标,<math>T^a</math>为基础表示中的<math>SU(3)</math> | + | 上式中<math>{\cal P}</math>为路径变序算子,它对几个算符乘积的作用效果为:将路径上更靠近终点的算子移动到左边,靠近起始点的算子移动到右边;a为色指标,<math>T^a</math>为基础表示中的<math>SU(3)</math>群生成元。夸克分布函数可以用如下的费曼图表示,其中<math>u^\mu=(0,1,\vec 0_\perp),~~~n\cdot A=A^+</math>。图中双线为eikonal线,它以及与胶子的相互作用节点均来自规范链。 |
| + | {|style="text-align: center;" | ||
| + | |[[文件:quark-pdf.png|300px]] || [[文件:pdf-eikonal.png|200px]] | ||
| + | |- | ||
| + | |夸克分布函数 || Eikonal线及与胶子的相互作用节点 | ||
| + | |} | ||
'''反夸克分布函数''' | '''反夸克分布函数''' | ||
| 第50行: | 第53行: | ||
\end{align}</math> | \end{align}</math> | ||
| − | [[文件:gluon-pdf.png|300px]] | + | {|style="text-align: center;" |
| − | + | |[[文件:gluon-pdf.png|300px]] | |
| + | |- | ||
| + | |胶子分布函数 | ||
| + | |} | ||
上式中<math>\tilde {\cal L}</math>为伴随表示中的规范链,形式与基础表示中的类似,只需将<math>T^a</math>替换为伴随表示中的<math>SU(3)</math>群生成元 <math>(T^a)_{bc}\equiv -if^{abc}</math>. | 上式中<math>\tilde {\cal L}</math>为伴随表示中的规范链,形式与基础表示中的类似,只需将<math>T^a</math>替换为伴随表示中的<math>SU(3)</math>群生成元 <math>(T^a)_{bc}\equiv -if^{abc}</math>. | ||
| + | |||
| + | 部分子分布函数在光锥规范中较明确的物理意义。光锥规范取<math> A^+=0</math>,规范链<math>{\cal L}=1</math>,[[济南大学粒子物理|规范势]],规范场强<math>F^{+\nu}=\partial^+A^\nu</math>。再利用光锥量子化的场算子 | ||
| + | |||
| + | <math>\begin{align} | ||
| + | \psi(x)=\int\frac{dk^+d^2k_\perp}{\sqrt{2p^+}\sqrt{(2\pi)^3}} \left[b_p^s u_p^s e^{-ik\cdot x}+d_p^{s\dagger} \bar v_p^s e^{ik\cdot x}\right]. | ||
| + | \end{align}</math> | ||
| + | |||
| + | 上式中<math>\left\{b_k^s,b_{k^\prime}^{s^\prime\dagger}\right\}=\left\{d_k^s,d_{k^\prime}^{s^\prime\dagger}\right\}=2k^+(2\pi)^3\delta(k^+-k^{\prime+})\delta^2(\vec k_\perp-\vec k^\prime_\perp)\delta^{ss^\prime}</math>。将其代入分布函数表达式,易得 | ||
| + | |||
| + | <math>f_q(x)\sim \langle p|\hat N_+(xp^+)+\hat N_-(xp^+)|p\rangle</math> | ||
| + | |||
| + | ,其中<math>\hat N_s(p)=b_p^{s\dagger}b_p^s</math> | ||
| + | |||
| + | == 极化的部分子分布函数 == | ||
| + | 考虑核子为极化的情况,描述核子极化方向的矢量为极化矢量<math>s^\mu</math>。在静止系中质子的自旋方向为<math>\vec{n}</math>,则极化矢量为<math>s_*^\mu=(0,\vec n)</math>,变换到运动系之后得到极化矢量为<math>s^\mu=\left(\frac{\vec p\cdot\vec n}{m},\vec n+\frac{(\vec p\cdot \vec n)\vec p}{m(m+p^0)}\right)</math>。对沿某个方向的粒子的极化投影算子为 | ||
| + | <math>\frac{1}{2}(1\pm\gamma_5 \not{s})</math>,其中<math>\pm</math>对应于正反粒子。Helicity 分布函数为 | ||
| + | |||
| + | <math>\begin{align} | ||
| + | \Delta q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\langle p,+|\bar\psi(0)\gamma^+\gamma_5{\cal L}(0,\xi^-)\psi(\xi^-)|p,+\rangle | ||
| + | \end{align}</math> | ||
| + | |||
| + | Transversity 分布函数为 | ||
| + | |||
| + | <math>\begin{align} | ||
| + | \delta q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\langle p,s_x^\uparrow|\bar\psi(0)\gamma_5\sigma^{+1}{\cal L}(0,\xi^-)\psi(\xi^-)|p,s_x^\uparrow\rangle | ||
| + | \end{align}</math> | ||
| + | |||
| + | 在光锥规范中,他们也有明确的物理意义 | ||
| + | |||
| + | <math>\begin{align} | ||
| + | \Delta q(x)\sim& \langle p|\hat N_+(xp^+)-\hat N_-(xp^+)|p\rangle\\ | ||
| + | \delta q(x)\sim& \langle p|\hat N_{s_x^\uparrow}(xp^+)-\hat N_{s_x^\downarrow}(xp^+)|p\rangle | ||
| + | \end{align}</math> | ||
| + | |||
| + | 即核子中不同自旋态的数密度之差。 | ||
| + | |||
| + | == 三维部分子分布函数 == | ||
| + | 如果某些物理过程对核子中夸克的内禀横动量比较敏感,我们就需要引入横动量依赖的三维部分子分布函数。根据洛伦兹不变性和空间反演不变性,在领头扭度,有8个三维夸克分布、8个三维反夸克分布和8个三维胶子分布,他们既描述了核子中带有特定横动量的部分子的数密度,也描写了核子横向自旋、核子动量与部分子的自旋、动量之间的关联。 | ||
| + | |||
| + | 对于三维部分子分布,高扭度(<math>(\Lambda/Q)</math>幂次压低的)贡献比较重要,我们需要讨论高扭度部分子分布函数。 | ||
| + | |||
| + | == 推广的部分子分布 == | ||
| + | |||
| + | 为了描述核子内夸克和胶子的角动量分布,人们引入了推广的部分子分布函数。 | ||
| + | |||
| + | == 角动量分布函数 == | ||
| + | == 核子自旋求和公式 == | ||
2021年6月13日 (日) 22:23的最后版本
概述
根据夸克模型,质子由三个夸夸uud组成,中子由三个夸克udd组成,自旋味道波函数为
$ \begin{align} |p,\uparrow\rangle=\frac{1}{\sqrt{18}}\left[uud(\uparrow\downarrow\uparrow+\downarrow\uparrow\uparrow-2\uparrow\uparrow\downarrow)+(\text{轮换})\right], \end{align} $
夸克质量约为300 MeV,处于$ L=0 $的基态,没有相对运动。
而根据部分子模型,质子由无穷数量的夸克、反夸克和胶子(统称为“部分子”)组成,组分之间的相互作用为量子色动力学(非微扰)。核子是一个具有无穷自由度的、强耦合多粒子系统。
核子结构研究的主要实验手段是高能粒子散射,如电子-核子深度非弹(DIS)、核子-核子碰撞的Drell-Yan过程、核子核子碰撞的大横动量强子/喷注产生等;主要理论工具为量子场论、量子色动力学及唯象模型等。近年来格点QCD在核子结构中的应用取得了突破性进展,在不久的将来将能够直接利用计算机模拟从QCD出发通过第一原理计算得到核子性质。
部分子分布函数
描述质子性质的物理量为部分子分布函数,他们给出了质子内某种部分子的数密度。光锥动量定义为$ p^\pm\equiv \frac{1}{\sqrt{2}}(p^0\pm p^z) $,假定质子沿z方向运动,则质子的四动量为$ \begin{align}p^\mu=\left(p^+,\frac{M^2}{2p^+},\vec 0_\perp\right)\end{align} $。
质子的夸克分布函数定义为
$ \begin{align} f_q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\left\langle p\left|\bar\psi_q(0){\cal L}(0,\xi^-)\gamma^+\psi_q(\xi^-)\right|p\right\rangle, \end{align} $
表示质子内动量分数为x、味道为q的夸克的数密度。上式中$ \displaystyle\langle p|\ldots|p\rangle\equiv \frac{1}{2}\sum_s\langle p,s|\ldots|p,s\rangle $, 出现的$ {\cal L} $为规范链,它的存在确保$ f_q(x) $为规范不变的物理观测量。规范链的定义为
$ \begin{align} {\cal L}(0,\xi^-)={\cal P}\exp\left\{-ig\int_0^{\xi^-} A^{a+}(\eta^-)T^ad\eta^-\right\} \end{align} $
上式中$ {\cal P} $为路径变序算子,它对几个算符乘积的作用效果为:将路径上更靠近终点的算子移动到左边,靠近起始点的算子移动到右边;a为色指标,$ T^a $为基础表示中的$ SU(3) $群生成元。夸克分布函数可以用如下的费曼图表示,其中$ u^\mu=(0,1,\vec 0_\perp),~~~n\cdot A=A^+ $。图中双线为eikonal线,它以及与胶子的相互作用节点均来自规范链。
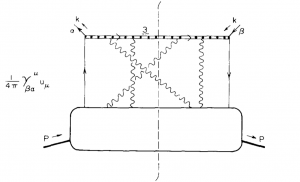 |
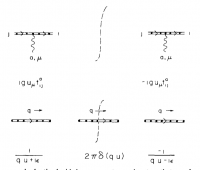
|
| 夸克分布函数 | Eikonal线及与胶子的相互作用节点 |
反夸克分布函数
$ \begin{align} f_\bar q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}{\rm Tr}[\gamma^+\left\langle p\left|\psi_q(0){\cal L}^\dagger (0,\xi^-)\bar\psi_q(\xi^-)\right|p\right\rangle. \end{align} $
根据费米子场的反对易性质,有 $ f_{\bar q}(x)=-f_q(-x) $.
胶子分布函数
$ \begin{align} G(x)=\frac{1}{xp^+}\int\frac{d\xi^-}{2\pi}e^{ixp^+\xi^-}\left\langle p\left|F^{+\nu}(0)\tilde{\cal L}(0,\xi^-){F_\nu}^+(\xi^-)\right|p\right\rangle. \end{align} $
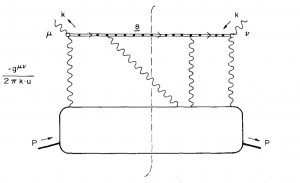
|
| 胶子分布函数 |
上式中$ \tilde {\cal L} $为伴随表示中的规范链,形式与基础表示中的类似,只需将$ T^a $替换为伴随表示中的$ SU(3) $群生成元 $ (T^a)_{bc}\equiv -if^{abc} $.
部分子分布函数在光锥规范中较明确的物理意义。光锥规范取$ A^+=0 $,规范链$ {\cal L}=1 $,规范势,规范场强$ F^{+\nu}=\partial^+A^\nu $。再利用光锥量子化的场算子
$ \begin{align} \psi(x)=\int\frac{dk^+d^2k_\perp}{\sqrt{2p^+}\sqrt{(2\pi)^3}} \left[b_p^s u_p^s e^{-ik\cdot x}+d_p^{s\dagger} \bar v_p^s e^{ik\cdot x}\right]. \end{align} $
上式中$ \left\{b_k^s,b_{k^\prime}^{s^\prime\dagger}\right\}=\left\{d_k^s,d_{k^\prime}^{s^\prime\dagger}\right\}=2k^+(2\pi)^3\delta(k^+-k^{\prime+})\delta^2(\vec k_\perp-\vec k^\prime_\perp)\delta^{ss^\prime} $。将其代入分布函数表达式,易得
$ f_q(x)\sim \langle p|\hat N_+(xp^+)+\hat N_-(xp^+)|p\rangle $
,其中$ \hat N_s(p)=b_p^{s\dagger}b_p^s $
极化的部分子分布函数
考虑核子为极化的情况,描述核子极化方向的矢量为极化矢量$ s^\mu $。在静止系中质子的自旋方向为$ \vec{n} $,则极化矢量为$ s_*^\mu=(0,\vec n) $,变换到运动系之后得到极化矢量为$ s^\mu=\left(\frac{\vec p\cdot\vec n}{m},\vec n+\frac{(\vec p\cdot \vec n)\vec p}{m(m+p^0)}\right) $。对沿某个方向的粒子的极化投影算子为 $ \frac{1}{2}(1\pm\gamma_5 \not{s}) $,其中$ \pm $对应于正反粒子。Helicity 分布函数为
$ \begin{align} \Delta q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\langle p,+|\bar\psi(0)\gamma^+\gamma_5{\cal L}(0,\xi^-)\psi(\xi^-)|p,+\rangle \end{align} $
Transversity 分布函数为
$ \begin{align} \delta q(x)=\int\frac{d\xi^-}{4\pi}e^{ixp^+\xi^-}\langle p,s_x^\uparrow|\bar\psi(0)\gamma_5\sigma^{+1}{\cal L}(0,\xi^-)\psi(\xi^-)|p,s_x^\uparrow\rangle \end{align} $
在光锥规范中,他们也有明确的物理意义
$ \begin{align} \Delta q(x)\sim& \langle p|\hat N_+(xp^+)-\hat N_-(xp^+)|p\rangle\\ \delta q(x)\sim& \langle p|\hat N_{s_x^\uparrow}(xp^+)-\hat N_{s_x^\downarrow}(xp^+)|p\rangle \end{align} $
即核子中不同自旋态的数密度之差。
三维部分子分布函数
如果某些物理过程对核子中夸克的内禀横动量比较敏感,我们就需要引入横动量依赖的三维部分子分布函数。根据洛伦兹不变性和空间反演不变性,在领头扭度,有8个三维夸克分布、8个三维反夸克分布和8个三维胶子分布,他们既描述了核子中带有特定横动量的部分子的数密度,也描写了核子横向自旋、核子动量与部分子的自旋、动量之间的关联。
对于三维部分子分布,高扭度($ (\Lambda/Q) $幂次压低的)贡献比较重要,我们需要讨论高扭度部分子分布函数。
推广的部分子分布
为了描述核子内夸克和胶子的角动量分布,人们引入了推广的部分子分布函数。