“数学物理方法”的版本间的差异

2021年6月9日 (三) 17:18的版本

800px

复变函数

复变函数可导的充要条件

$ f(z)=u(x,y)+iv(x,y) $可导的充要条件为：偏导$ \frac{\partial u}{\partial x} $、$ \frac{\partial u}{\partial y} $、$ \frac{\partial v}{\partial x} $、$ \frac{\partial v}{\partial y} $存在、连续，且满足柯西-黎曼条件。

柯西-黎曼条件

1. 笛卡尔系 ：$ \begin{align}\left\{\begin{array}{l} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\\ \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} \end{array}\right.\end{align} $
2. 极坐标系：$ \begin{align}\left\{\begin{array}{l} \frac{\partial u}{\partial \rho}=\frac{1}{\rho}\frac{\partial v}{\partial \varphi},\\ \frac{1}{\rho}\frac{\partial u}{\partial \varphi}=-\frac{\partial v}{\partial \rho}. \end{array}\right.\end{align} $

已知实部（虚部）求虚部（实部）

一般解法：曲线积分法。

复变函数积分

幂级数展开

留数定理

傅里叶变换

傅里叶展开小结

$ \begin{align}f(x)=\left\{\begin{array}{ll} \sum_{n=1}^\infty B_k\sin\frac{n\pi x}{l},&~~~(f(0)=f(l)=0)\\ \sum_{n=0}^\infty B_k\sin\frac{(n+1/2)\pi x}{l},&~~~(f(0)=f'(l)=0)\\ \sum_{n=0}^\infty A_k\cos\frac{(n+1/2)n\pi x}{l},&~~~(f'(0)=f(l)=0)\\ \sum_{n=0}^\infty A_k\cos\frac{n\pi x}{l}.&~~~(f'(0)=f'(l)=0) \end{array}\right.\end{align} $

常用公式

傅里叶展开的时候，经常涉及到形如$ \int_0^1\xi^n\sin\lambda \xi{\rm d}\xi $和$ \int_0^1\xi^n\cos\lambda\xi{\rm d}\xi $的积分。可以利用$ \xi^ne^{i\lambda\xi}=\frac{1}{i^n}\frac{{\rm d}^n}{{\rm d}\lambda^n}e^{i\lambda\xi} $，将其化简。最终结果为，

$ \begin{align} \int_0^1\xi^n\sin\lambda\xi{\rm d}\xi=\left\{\begin{array}{ll} (-1)^{k+1}\frac{{\rm d}^{2k+1}}{{\rm d}\lambda^{2k+1}}\frac{\sin\lambda}{\lambda},&(n=2k+1)\\ (-1)^{k+1}\frac{{\rm d}^{2k}}{{\rm d}\lambda^{2k}}\frac{\cos\lambda-1}{\lambda},&(n=2k) \end{array}\right.~~~(k=0,1,2,\ldots)\end{align} $ $ \begin{align} \int_0^1\xi^n\cos\lambda\xi{\rm d}\xi=\left\{\begin{array}{ll} (-1)^{k+1}\frac{{\rm d}^{2k+1}}{{\rm d}\lambda^{2k+1}}\frac{\cos\lambda-1}{\lambda},&(n=2k+1)\\ (-1)^{k}\frac{{\rm d}^{2k}}{{\rm d}\lambda^{2k}}\frac{\sin\lambda}{\lambda},&(n=2k) \end{array}\right.~~~(k=0,1,2,\ldots) \end{align} $

拉普拉斯变换

$ \bar f(p)=\int_0^\infty f(t)e^{-pt}{\rm d}t $， $ ~~~~~~({\rm Re}p>0 $；$ {\rm Re}p $足够大，使得变换收敛$ ) $

$ {\cal L}[t^ne^{st}]=\frac{n!}{(p-s)^{n+1}}, $

$ {\cal L}[t^nf(t)]=(-1)^n\frac{{\rm d}^n}{{\rm d}p^n}\bar f(p). $

数学物理定解问题

分离变数法

级数解法、本征值问题

球函数

轴对称情形

$ u(r,\theta)=\sum_{l=0}^\infty\left(A_l r^l+\frac{B_l}{r^{l+1}}\right) {\rm P}_l(\cos\theta) $

一般情形

$ \begin{align} u(r,\theta,\varphi)=&\sum_{m=0}^\infty \sum_{l=m}^\infty\left(A_l^m r^l+\frac{B_l^m}{r^{l+1}}\right) {\rm P}_l^m(\cos\theta)\cos m\varphi\\ &+\sum_{m=1}^\infty \sum_{l=m}^\infty\left(C_l^m r^l+\frac{D_l^m}{r^{l+1}}\right) {\rm P}_l^m(\cos\theta)\sin m\varphi \end{align} $

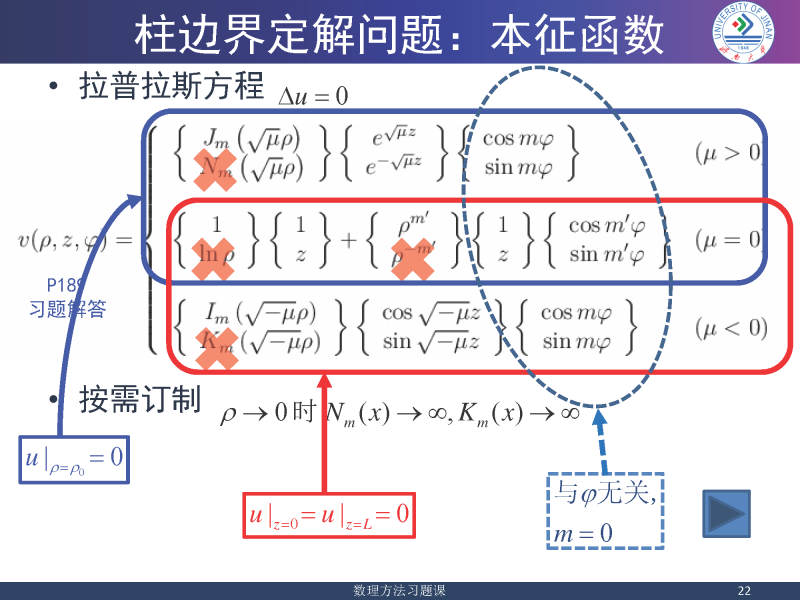
柱函数

格林函数法

主要思想

$ \begin{align} \left\{ \begin{array}{l} \Delta u=f({\bf r}),\\ \left.\left(\alpha \frac{\partial u}{\partial n}+\beta u\right)\right|_\Sigma=\varphi(M), \end{array} \right. \end{align} $

转化为求解格林函数边值问题

第一类边界条件：$ \begin{align}&\left\{\begin{array}{l} \Delta G=\delta({\bf r}-{\bf r}_0),\\ G|_\Sigma=0, \end{array} \right.&&u({\bf r})=\iiint_TG({\bf r},{\bf r}_0)f({\bf r}_0){\rm d} V_0+\iint_{\Sigma}\varphi({\bf r_0})\frac{\partial G({\bf r},{\bf r}_0)}{\partial n_0}{\rm d} S_0, \end{align} $

第二类边界条件：$ \begin{align} \left\{ \begin{array}{l} \Delta G=\delta({\bf r}-{\bf r}_0)-\frac{1}{V_T},\\ \frac{\partial G}{\partial n}|_\Sigma=0, \end{array} \right.&&u({\bf r})=\iiint_TG({\bf r},{\bf r}_0)f({\bf r}_0){\rm d} V_0-\iint_{\Sigma}\varphi({\bf r_0})G({\bf r},{\bf r}_0){\rm d} S_0,\end{align} $

第三类边界条件： $ \begin{align} \left\{ \begin{array}{l} \Delta G=\delta({\bf r}-{\bf r}_0),\\ \left(\alpha \frac{\partial G}{\partial n}+\beta G\right)|_\Sigma=0, \end{array} \right.&&u({\bf r})=\iiint_TG({\bf r},{\bf r}_0)f({\bf r}_0){\rm d} V_0-\frac{1}{\alpha}\iint_{\Sigma}\varphi({\bf r_0})G({\bf r},{\bf r}_0){\rm d} S_0, \end{align} $

积分变换法

保角变换法

非线性数学物理问题简介